Regional model

This example shows a simplified script for building a groundwater model in the northeast of the Netherlands. A primary feature of this area is an ice-pushed ridge called the Hondsrug. This examples demonstrates modifying external data for use in a MODFLOW 6 model.

In overview, the model features:

• Thirteen layers: seven aquifers and six aquitards;

• A dense ditch network in the east;

• Pipe drainage for agriculture;

• Precipitation and evapotranspiration.

We’ll start with the usual imports, and an import from scipy.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.ndimage
import xarray as xr

import imod

Before starting to create the input data, we will create the groundwater imod.mf6.GroundwaterFlowModel. The data from all the model packages will be added to this variable.

gwf_model = imod.mf6.GroundwaterFlowModel()

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 37, in <module>
    gwf_model = imod.mf6.GroundwaterFlowModel()
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterFlowModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 37, in <module>
    gwf_model = imod.mf6.GroundwaterFlowModel()
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 120, in __init__
    self._validate_init_schemata_options(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()

This package allows specifying a regular MODFLOW grid. This grid is assumed to be rectangular horizontally, but can be distorted vertically.

Load data

We’ll load the data from the examples that come with this package.

layermodel = imod.data.hondsrug_layermodel()

# Make sure that the idomain is provided as integers
idomain = layermodel["idomain"].astype(int)

# We only need to provide the data for the top as a 2D array. MODFLOW 6 will
# compare the top against the uppermost active bottom cell.
top = layermodel["top"].max(dim="layer")

bot = layermodel["bottom"]

top.plot.imshow()

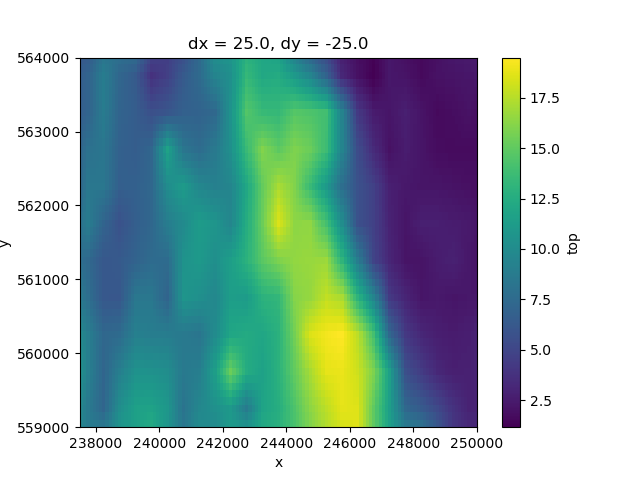
<matplotlib.image.AxesImage object at 0x000001466DC49590>

Adding information to the DIS package

The following step is to add the previously created discretization data to the gwf_model variable. This is done using the function imod.mf6.StructuredDiscretization. The data to include is the top of the model domain, the bottom of the layers, and the idomain. All this information comes from the previously imported tifs (now converted to xarray.DataArray.

gwf_model["dis"] = imod.mf6.StructuredDiscretization(
    top=top, bottom=bot, idomain=idomain
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 73, in <module>
    gwf_model["dis"] = imod.mf6.StructuredDiscretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the StructuredDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 73, in <module>
    gwf_model["dis"] = imod.mf6.StructuredDiscretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 125, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()

Node property flow package - NPF

This package contains the information related to the aquifer properties used to calculate hydraulic conductance. This package replaces the Layer Property Flow (LPF), Block-Centered Flow (BCF), and Upstream Weighting (UPW) packages from previous MODFLOW versions.

Hydraulic conductivity

k = layermodel["k"]

icelltype

The cell type to be used in the model (confined or convertible) can be defined under ICELLTYPE, which is an input to the NPF package. ICELLTYPE == 0: Confined cell - Constant transmissivity ICELLTYPE != 0: Convertible cell - Transmissivity varies depending on the calculated head in the cell (based on the saturated cell thickness)

In this example, all layers have a ICELLTYPE equal to 0, indicating confined cells. This is defined in the following section.

Adding information to the NPF package

The information for the NPF package is added to the gwf_model variable using imod.mf6.NodePropertyFlow. The information included is the icelltype value (equal to zero), the array for the hydraulic conductivity (considered to be the same for the horizontal and vertical direction) and, optionally, the variable_vertical_conductance, dewatered, perched and save_flows options have been activated. For more details about the meaning of these variables and other variables available to be used within this package, please refer to the documentation.

gwf_model["npf"] = imod.mf6.NodePropertyFlow(
    icelltype=0,
    k=k,
    k33=k,
    variable_vertical_conductance=True,
    dewatered=True,
    perched=True,
    save_flows=True,
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 116, in <module>
    gwf_model["npf"] = imod.mf6.NodePropertyFlow(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the NodePropertyFlow package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 116, in <module>
    gwf_model["npf"] = imod.mf6.NodePropertyFlow(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 423, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()

Initial conditions package - IC

This package reads the starting heads for a simulation.

Starting heads interpolation

The starting heads to be used in this model are based on the interpolation of x-y head measurements, which were interpolated on a larger area. This example was created in this example –insert-link-here–

The heads were interpolated on a larger area, therefore these have to be clipped first

initial = imod.data.hondsrug_initial()
interpolated_head_larger = initial["head"]

xmin = 237_500.0
xmax = 250_000.0
ymin = 559_000.0
ymax = 564_000.0

interpolated_head = interpolated_head_larger.sel(
    x=slice(xmin, xmax), y=slice(ymax, ymin)
)

# Plotting the clipped interpolation
fig, ax = plt.subplots()
interpolated_head.plot.imshow(ax=ax)

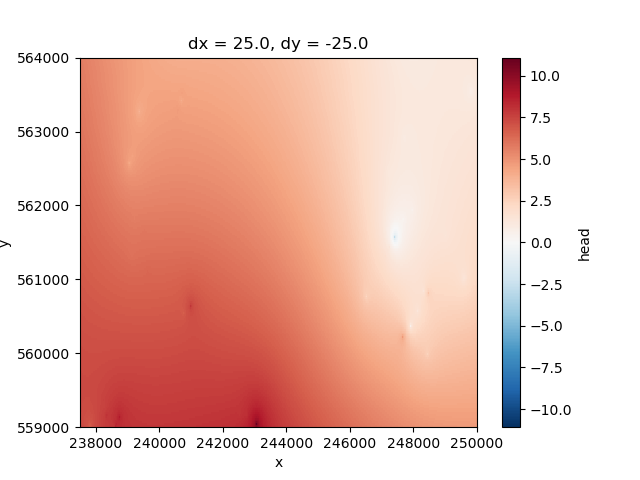
<matplotlib.image.AxesImage object at 0x00000146746365D0>

The final step is to assign the 2D heads interpolation to all the model layers (as a reference value) by using the xarray tool xarray.full_like. The 3d idomain array is used as reference for the geometry and then its original values are replaced by NaNs. This array is combined with the interpolated_head array using the xarray DataArray.combine_first option. The final result is an starting_heads xarray where all layers have the 2d interpolated_head information.

# Assign interpolated head values to all the model layers
like_3d = xr.full_like(idomain, np.nan, dtype=float)
starting_head = like_3d.combine_first(interpolated_head)
# Consequently ensure no data is specified in inactive cells:
starting_head = starting_head.where(idomain == 1)

starting_head

<xarray.DataArray 'idomain' (layer: 13, y: 200, x: 500)> Size: 10MB
array([[[       nan,        nan,        nan, ..., 1.27008811,
         1.27823924, 1.28676046],
        [       nan,        nan,        nan, ..., 1.26336139,
         1.27183901, 1.28070347],
        [       nan,        nan,        nan, ..., 1.25620192,
         1.26504986, 1.27431479],
        ...,
        [7.28608515, 7.26550211, 7.24273429, ...,        nan,
                nan,        nan],
        [7.2907364 , 7.26985601, 7.24672249, ...,        nan,
                nan,        nan],
        [7.29728577, 7.27649525, 7.25355321, ...,        nan,
                nan,        nan]],

       [[       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
...
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan],
        [       nan,        nan,        nan, ...,        nan,
                nan,        nan]],

       [[5.6706604 , 5.65319374, 5.63573351, ..., 1.27008811,
         1.27823924, 1.28676046],
        [5.67764711, 5.66021213, 5.64275829, ..., 1.26336139,
         1.27183901, 1.28070347],
        [5.68462064, 5.66720984, 5.64976361, ..., 1.25620192,
         1.26504986, 1.27431479],
        ...,
        [7.28608515, 7.26550211, 7.24273429, ..., 4.67051889,
         4.66997651, 4.66944365],
        [7.2907364 , 7.26985601, 7.24672249, ..., 4.70303061,
         4.70234778, 4.70168152],
        [7.29728577, 7.27649525, 7.25355321, ..., 4.73551559,
         4.73469247, 4.73389453]]], shape=(13, 200, 500))
Coordinates:
  * layer    (layer) int32 52B 1 2 3 4 5 6 7 8 9 10 11 12 13
  * y        (y) float64 2kB 5.64e+05 5.64e+05 5.639e+05 ... 5.59e+05 5.59e+05
  * x        (x) float64 4kB 2.375e+05 2.375e+05 2.376e+05 ... 2.5e+05 2.5e+05
    dx       float64 8B 25.0
    dy       float64 8B -25.0

xarray.DataArray

'idomain'

• layer: 13
• y: 200
• x: 500

• nan nan nan nan nan nan nan ... 4.738 4.737 4.736 4.736 4.735 4.734

  array([[[       nan,        nan,        nan, ..., 1.27008811,
           1.27823924, 1.28676046],
          [       nan,        nan,        nan, ..., 1.26336139,
           1.27183901, 1.28070347],
          [       nan,        nan,        nan, ..., 1.25620192,
           1.26504986, 1.27431479],
          ...,
          [7.28608515, 7.26550211, 7.24273429, ...,        nan,
                  nan,        nan],
          [7.2907364 , 7.26985601, 7.24672249, ...,        nan,
                  nan,        nan],
          [7.29728577, 7.27649525, 7.25355321, ...,        nan,
                  nan,        nan]],
  
         [[       nan,        nan,        nan, ...,        nan,
                  nan,        nan],
          [       nan,        nan,        nan, ...,        nan,
                  nan,        nan],
          [       nan,        nan,        nan, ...,        nan,
                  nan,        nan],
  ...
          [       nan,        nan,        nan, ...,        nan,
                  nan,        nan],
          [       nan,        nan,        nan, ...,        nan,
                  nan,        nan],
          [       nan,        nan,        nan, ...,        nan,
                  nan,        nan]],
  
         [[5.6706604 , 5.65319374, 5.63573351, ..., 1.27008811,
           1.27823924, 1.28676046],
          [5.67764711, 5.66021213, 5.64275829, ..., 1.26336139,
           1.27183901, 1.28070347],
          [5.68462064, 5.66720984, 5.64976361, ..., 1.25620192,
           1.26504986, 1.27431479],
          ...,
          [7.28608515, 7.26550211, 7.24273429, ..., 4.67051889,
           4.66997651, 4.66944365],
          [7.2907364 , 7.26985601, 7.24672249, ..., 4.70303061,
           4.70234778, 4.70168152],
          [7.29728577, 7.27649525, 7.25355321, ..., 4.73551559,
           4.73469247, 4.73389453]]], shape=(13, 200, 500))

• Coordinates: (5)
  • layer
    (layer)
    int32
    1 2 3 4 5 6 7 8 9 10 11 12 13

    array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13], dtype=int32)

  • y
    (y)
    float64
    5.64e+05 5.64e+05 ... 5.59e+05

    array([563987.5, 563962.5, 563937.5, 563912.5, 563887.5, 563862.5, 563837.5,
           563812.5, 563787.5, 563762.5, 563737.5, 563712.5, 563687.5, 563662.5,
           563637.5, 563612.5, 563587.5, 563562.5, 563537.5, 563512.5, 563487.5,
           563462.5, 563437.5, 563412.5, 563387.5, 563362.5, 563337.5, 563312.5,
           563287.5, 563262.5, 563237.5, 563212.5, 563187.5, 563162.5, 563137.5,
           563112.5, 563087.5, 563062.5, 563037.5, 563012.5, 562987.5, 562962.5,
           562937.5, 562912.5, 562887.5, 562862.5, 562837.5, 562812.5, 562787.5,
           562762.5, 562737.5, 562712.5, 562687.5, 562662.5, 562637.5, 562612.5,
           562587.5, 562562.5, 562537.5, 562512.5, 562487.5, 562462.5, 562437.5,
           562412.5, 562387.5, 562362.5, 562337.5, 562312.5, 562287.5, 562262.5,
           562237.5, 562212.5, 562187.5, 562162.5, 562137.5, 562112.5, 562087.5,
           562062.5, 562037.5, 562012.5, 561987.5, 561962.5, 561937.5, 561912.5,
           561887.5, 561862.5, 561837.5, 561812.5, 561787.5, 561762.5, 561737.5,
           561712.5, 561687.5, 561662.5, 561637.5, 561612.5, 561587.5, 561562.5,
           561537.5, 561512.5, 561487.5, 561462.5, 561437.5, 561412.5, 561387.5,
           561362.5, 561337.5, 561312.5, 561287.5, 561262.5, 561237.5, 561212.5,
           561187.5, 561162.5, 561137.5, 561112.5, 561087.5, 561062.5, 561037.5,
           561012.5, 560987.5, 560962.5, 560937.5, 560912.5, 560887.5, 560862.5,
           560837.5, 560812.5, 560787.5, 560762.5, 560737.5, 560712.5, 560687.5,
           560662.5, 560637.5, 560612.5, 560587.5, 560562.5, 560537.5, 560512.5,
           560487.5, 560462.5, 560437.5, 560412.5, 560387.5, 560362.5, 560337.5,
           560312.5, 560287.5, 560262.5, 560237.5, 560212.5, 560187.5, 560162.5,
           560137.5, 560112.5, 560087.5, 560062.5, 560037.5, 560012.5, 559987.5,
           559962.5, 559937.5, 559912.5, 559887.5, 559862.5, 559837.5, 559812.5,
           559787.5, 559762.5, 559737.5, 559712.5, 559687.5, 559662.5, 559637.5,
           559612.5, 559587.5, 559562.5, 559537.5, 559512.5, 559487.5, 559462.5,
           559437.5, 559412.5, 559387.5, 559362.5, 559337.5, 559312.5, 559287.5,
           559262.5, 559237.5, 559212.5, 559187.5, 559162.5, 559137.5, 559112.5,
           559087.5, 559062.5, 559037.5, 559012.5])

  • x
    (x)
    float64
    2.375e+05 2.375e+05 ... 2.5e+05

    array([237512.5, 237537.5, 237562.5, ..., 249937.5, 249962.5, 249987.5],
          shape=(500,))

  • dx
    ()
    float64
    25.0

    array(25.)

  • dy
    ()
    float64
    -25.0

    array(-25.)

Adding information to the IC package

The function for indicating the initial conditions is imod.mf6.InitialConditions. It is necessary to indicate the value(s) to be considered as the initial (starting) head of the simulation. In this case, this value is equal to the previously created starting_head array.

gwf_model["ic"] = imod.mf6.InitialConditions(starting_head)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 187, in <module>
    gwf_model["ic"] = imod.mf6.InitialConditions(starting_head)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 187, in <module>
    gwf_model["ic"] = imod.mf6.InitialConditions(starting_head)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()

Constant head package - CHD

This package allows to indicate if the head varies with time, if it is constant or if it is inactive.

Constant head edge

The previously interpolated starting_head array will be used to define the constant head value which will be used along the model boundaries. A function is defined to indicate the location of the outer edge (returning a boolean array).

def outer_edge(da):
    data = da.copy()
    from_edge = scipy.ndimage.binary_erosion(data)
    is_edge = (data == 1) & (from_edge == 0)
    return is_edge.astype(bool)

For the next calculations, it is necessary to create a template array which can be used for assigning the corresponding geometry to other arrays. In this case, a 2d template is created based on the idomain layer information and filled with ones.

like_2d = xr.full_like(idomain.isel(layer=0), 1)
like_2d

<xarray.DataArray 'idomain' (y: 200, x: 500)> Size: 800kB
array([[1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       ...,
       [1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1],
       [1, 1, 1, ..., 1, 1, 1]], shape=(200, 500))
Coordinates:
  * y        (y) float64 2kB 5.64e+05 5.64e+05 5.639e+05 ... 5.59e+05 5.59e+05
  * x        (x) float64 4kB 2.375e+05 2.375e+05 2.376e+05 ... 2.5e+05 2.5e+05
    dx       float64 8B 25.0
    dy       float64 8B -25.0
    layer    int32 4B 1

xarray.DataArray

'idomain'

• y: 200
• x: 500

• 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

  array([[1, 1, 1, ..., 1, 1, 1],
         [1, 1, 1, ..., 1, 1, 1],
         [1, 1, 1, ..., 1, 1, 1],
         ...,
         [1, 1, 1, ..., 1, 1, 1],
         [1, 1, 1, ..., 1, 1, 1],
         [1, 1, 1, ..., 1, 1, 1]], shape=(200, 500))

• Coordinates: (5)
  • y
    (y)
    float64
    5.64e+05 5.64e+05 ... 5.59e+05

    array([563987.5, 563962.5, 563937.5, 563912.5, 563887.5, 563862.5, 563837.5,
           563812.5, 563787.5, 563762.5, 563737.5, 563712.5, 563687.5, 563662.5,
           563637.5, 563612.5, 563587.5, 563562.5, 563537.5, 563512.5, 563487.5,
           563462.5, 563437.5, 563412.5, 563387.5, 563362.5, 563337.5, 563312.5,
           563287.5, 563262.5, 563237.5, 563212.5, 563187.5, 563162.5, 563137.5,
           563112.5, 563087.5, 563062.5, 563037.5, 563012.5, 562987.5, 562962.5,
           562937.5, 562912.5, 562887.5, 562862.5, 562837.5, 562812.5, 562787.5,
           562762.5, 562737.5, 562712.5, 562687.5, 562662.5, 562637.5, 562612.5,
           562587.5, 562562.5, 562537.5, 562512.5, 562487.5, 562462.5, 562437.5,
           562412.5, 562387.5, 562362.5, 562337.5, 562312.5, 562287.5, 562262.5,
           562237.5, 562212.5, 562187.5, 562162.5, 562137.5, 562112.5, 562087.5,
           562062.5, 562037.5, 562012.5, 561987.5, 561962.5, 561937.5, 561912.5,
           561887.5, 561862.5, 561837.5, 561812.5, 561787.5, 561762.5, 561737.5,
           561712.5, 561687.5, 561662.5, 561637.5, 561612.5, 561587.5, 561562.5,
           561537.5, 561512.5, 561487.5, 561462.5, 561437.5, 561412.5, 561387.5,
           561362.5, 561337.5, 561312.5, 561287.5, 561262.5, 561237.5, 561212.5,
           561187.5, 561162.5, 561137.5, 561112.5, 561087.5, 561062.5, 561037.5,
           561012.5, 560987.5, 560962.5, 560937.5, 560912.5, 560887.5, 560862.5,
           560837.5, 560812.5, 560787.5, 560762.5, 560737.5, 560712.5, 560687.5,
           560662.5, 560637.5, 560612.5, 560587.5, 560562.5, 560537.5, 560512.5,
           560487.5, 560462.5, 560437.5, 560412.5, 560387.5, 560362.5, 560337.5,
           560312.5, 560287.5, 560262.5, 560237.5, 560212.5, 560187.5, 560162.5,
           560137.5, 560112.5, 560087.5, 560062.5, 560037.5, 560012.5, 559987.5,
           559962.5, 559937.5, 559912.5, 559887.5, 559862.5, 559837.5, 559812.5,
           559787.5, 559762.5, 559737.5, 559712.5, 559687.5, 559662.5, 559637.5,
           559612.5, 559587.5, 559562.5, 559537.5, 559512.5, 559487.5, 559462.5,
           559437.5, 559412.5, 559387.5, 559362.5, 559337.5, 559312.5, 559287.5,
           559262.5, 559237.5, 559212.5, 559187.5, 559162.5, 559137.5, 559112.5,
           559087.5, 559062.5, 559037.5, 559012.5])

  • x
    (x)
    float64
    2.375e+05 2.375e+05 ... 2.5e+05

    array([237512.5, 237537.5, 237562.5, ..., 249937.5, 249962.5, 249987.5],
          shape=(500,))

  • dx
    ()
    float64
    25.0

    array(25.)

  • dy
    ()
    float64
    -25.0

    array(-25.)

  • layer
    ()
    int32
    1

    array(1, dtype=int32)

Using the previously created function and the 2d template, the outer edge is defined for this example.

edge = outer_edge(xr.full_like(like_2d.drop_vars("layer"), 1))

Adding information to the CHD package

To add the information to the CHD package within the gwf_model variable, the imod.mf6.ConstantHead. function is used. The required information is the head array for this boundary condition. In this example, the starting_head array is selected where the idomain is > 0 (active) and it is located in the edge array.

It is also possible (and optional) to indicate if the CHD information will be written to the listing file after it is read (print_input), if the constant head flow rates will be printed to the listing file for every stress period time step in which “BUDGET PRINT” is specified in Output Control (print_flows) and if the constant head flow terms will be written to the file specified with “BUDGET FILEOUT” in Output Control (save_flows). By default, these three options are set to False.

gwf_model["chd"] = imod.mf6.ConstantHead(
    starting_head.where((idomain > 0) & edge),
    print_input=False,
    print_flows=True,
    save_flows=True,
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 246, in <module>
    gwf_model["chd"] = imod.mf6.ConstantHead(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantHead package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 246, in <module>
    gwf_model["chd"] = imod.mf6.ConstantHead(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 152, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()

Recharge

This package is used to represent areally distributed recharge to the groundwater system. To calculate the recharge, the precipitation and evapotranspiration information from the KNMI website has been downloaded for the study area. This information is saved in netCDF files, which have been imported using the xarray function xr.open_dataset, slicing the area to the model’s miminum and maximum dimensions.

Note that the meteorological data has mm/d as unit and this has to be converted to m/d for MODFLOW 6.

xmin = 230_000.0
xmax = 257_000.0
ymin = 550_000.0
ymax = 567_000.0

meteorology = imod.data.hondsrug_meteorology()
pp = meteorology["precipitation"]
evt = meteorology["evapotranspiration"]

pp = pp.sel(x=slice(xmin, xmax), y=slice(ymax, ymin)) / 1000.0  # from mm/d to m/d
evt = evt.sel(x=slice(xmin, xmax), y=slice(ymax, ymin)) / 1000.0  # from mm/d to m/d

Recharge - Steady state

For the steady state conditions of the model, the data from the period 2000 to 2009 was considered as reference. The initial information was sliced to this time period and averaged to obtain the a mean value grid. This process was done for both precipitation and evapotranspiration datasets.

Precipitation

pp_ss = pp.sel(time=slice("2000-01-01", "2009-12-31"))
pp_ss_mean = pp_ss.mean(dim="time")

fig, ax = plt.subplots()
pp_ss_mean.plot(ax=ax)

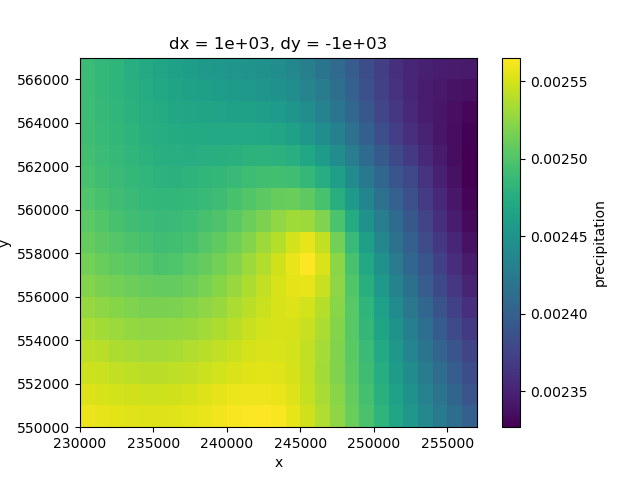
<matplotlib.collections.QuadMesh object at 0x000001467057A5D0>

Evapotranspiration

evt_ss = evt.sel(time=slice("2000-01-01", "2009-12-31"))
evt_ss_mean = evt_ss.mean(dim="time")

fig, ax = plt.subplots()
evt_ss_mean.plot(ax=ax)

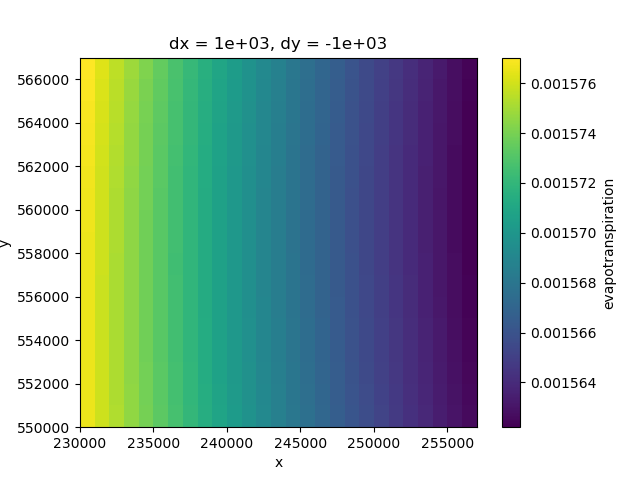
<matplotlib.collections.QuadMesh object at 0x00000146415DED50>

For the recharge calculation, a first estimate is the difference between the precipitation and evapotranspiration values.

rch_ss = pp_ss_mean - evt_ss_mean

fig, ax = plt.subplots()
rch_ss.plot.imshow(ax=ax)

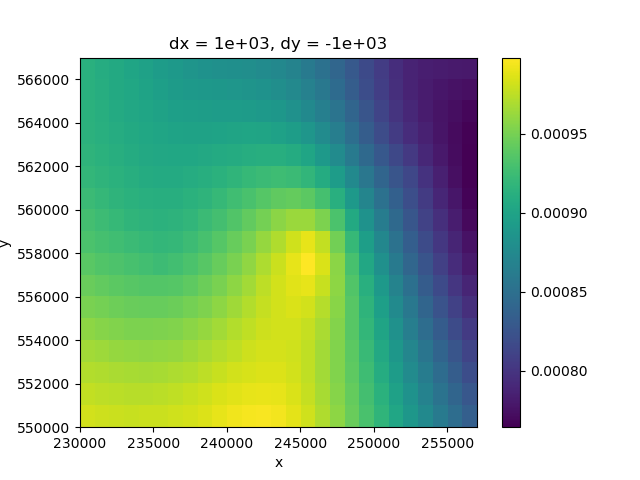
<matplotlib.image.AxesImage object at 0x000001466AC13D90>

Recharge - Transient

The transient model will encompass the period from 2010 to 2015. The initial pp and evt datasets have been sliced to this time frame.

pp_trans = pp.sel(time=slice("2010-01-01", "2015-12-31"))
evt_trans = evt.sel(time=slice("2010-01-01", "2015-12-31"))

As previously done, it is assumed that the recharge is equal to the difference between precipitation and evapotranspiration as a first estimate. Furthermore, the negative values found after doing this calculation have been replaced by zeros, as the recharge should not have a negative value.

rch_trans = pp_trans - evt_trans
rch_trans = rch_trans.where(rch_trans > 0, 0)  # check negative values

The original information is on a daily step, so it is going to be resampled to a yearly step by using the xarray function Dataset.resample.

rch_trans_yr = rch_trans.resample(time="YS", label="left").mean()
rch_trans_yr

<xarray.DataArray (time: 6, y: 17, x: 27)> Size: 11kB
array([[[0.00191725, 0.00191589, 0.00191248, ..., 0.00158879,
         0.00160275, 0.00161772],
        [0.00193096, 0.00193016, 0.0019277 , ..., 0.00159777,
         0.00160856, 0.00162071],
        [0.00194592, 0.00194606, 0.00194384, ..., 0.00160863,
         0.00161658, 0.0016263 ],
        ...,
        [0.00205102, 0.0020491 , 0.00204451, ..., 0.00175834,
         0.00175477, 0.00175247],
        [0.0020481 , 0.00204493, 0.00203995, ..., 0.00177083,
         0.0017666 , 0.00176362],
        [0.00204444, 0.002041  , 0.00203658, ..., 0.00178251,
         0.00177807, 0.00177411]],

       [[0.00175232, 0.0017549 , 0.00175632, ..., 0.00160428,
         0.0016166 , 0.00163142],
        [0.00175832, 0.00176321, 0.00176716, ..., 0.00161909,
         0.00162744, 0.00163787],
        [0.00176593, 0.00177297, 0.00177865, ..., 0.00163613,
         0.00164029, 0.00164618],
...
        [0.00190413, 0.0019    , 0.00189647, ..., 0.00168478,
         0.00167463, 0.00166721],
        [0.00191761, 0.00191336, 0.00190866, ..., 0.00169624,
         0.00168655, 0.0016792 ],
        [0.0019308 , 0.00192603, 0.0019212 , ..., 0.00170712,
         0.00169771, 0.00169032]],

       [[0.00226806, 0.00225167, 0.00223808, ..., 0.00221006,
         0.00219559, 0.00218172],
        [0.0022924 , 0.00227892, 0.00226807, ..., 0.00220936,
         0.00219364, 0.00217812],
        [0.00231699, 0.00230603, 0.00229702, ..., 0.00221065,
         0.0021932 , 0.00217596],
        ...,
        [0.00249076, 0.00248442, 0.00247622, ..., 0.00224485,
         0.00222806, 0.00221361],
        [0.00249192, 0.00248449, 0.00247561, ..., 0.00224585,
         0.00223096, 0.00221743],
        [0.00249155, 0.00248376, 0.00247603, ..., 0.00224736,
         0.00223372, 0.00222133]]], shape=(6, 17, 27), dtype=float32)
Coordinates:
  * time     (time) datetime64[ns] 48B 2010-01-01 2011-01-01 ... 2015-01-01
  * y        (y) float64 136B 5.665e+05 5.655e+05 ... 5.515e+05 5.505e+05
  * x        (x) float64 216B 2.305e+05 2.315e+05 ... 2.555e+05 2.565e+05
    dx       float64 8B 1e+03
    dy       float64 8B -1e+03
Attributes:
    units:    mm/d

xarray.DataArray

• time: 6
• y: 17
• x: 27

• 0.001917 0.001916 0.001912 0.001907 ... 0.002247 0.002234 0.002221

  array([[[0.00191725, 0.00191589, 0.00191248, ..., 0.00158879,
           0.00160275, 0.00161772],
          [0.00193096, 0.00193016, 0.0019277 , ..., 0.00159777,
           0.00160856, 0.00162071],
          [0.00194592, 0.00194606, 0.00194384, ..., 0.00160863,
           0.00161658, 0.0016263 ],
          ...,
          [0.00205102, 0.0020491 , 0.00204451, ..., 0.00175834,
           0.00175477, 0.00175247],
          [0.0020481 , 0.00204493, 0.00203995, ..., 0.00177083,
           0.0017666 , 0.00176362],
          [0.00204444, 0.002041  , 0.00203658, ..., 0.00178251,
           0.00177807, 0.00177411]],
  
         [[0.00175232, 0.0017549 , 0.00175632, ..., 0.00160428,
           0.0016166 , 0.00163142],
          [0.00175832, 0.00176321, 0.00176716, ..., 0.00161909,
           0.00162744, 0.00163787],
          [0.00176593, 0.00177297, 0.00177865, ..., 0.00163613,
           0.00164029, 0.00164618],
  ...
          [0.00190413, 0.0019    , 0.00189647, ..., 0.00168478,
           0.00167463, 0.00166721],
          [0.00191761, 0.00191336, 0.00190866, ..., 0.00169624,
           0.00168655, 0.0016792 ],
          [0.0019308 , 0.00192603, 0.0019212 , ..., 0.00170712,
           0.00169771, 0.00169032]],
  
         [[0.00226806, 0.00225167, 0.00223808, ..., 0.00221006,
           0.00219559, 0.00218172],
          [0.0022924 , 0.00227892, 0.00226807, ..., 0.00220936,
           0.00219364, 0.00217812],
          [0.00231699, 0.00230603, 0.00229702, ..., 0.00221065,
           0.0021932 , 0.00217596],
          ...,
          [0.00249076, 0.00248442, 0.00247622, ..., 0.00224485,
           0.00222806, 0.00221361],
          [0.00249192, 0.00248449, 0.00247561, ..., 0.00224585,
           0.00223096, 0.00221743],
          [0.00249155, 0.00248376, 0.00247603, ..., 0.00224736,
           0.00223372, 0.00222133]]], shape=(6, 17, 27), dtype=float32)

• Coordinates: (5)
  • time
    (time)
    datetime64[ns]
    2010-01-01 ... 2015-01-01

    array(['2010-01-01T00:00:00.000000000', '2011-01-01T00:00:00.000000000',
           '2012-01-01T00:00:00.000000000', '2013-01-01T00:00:00.000000000',
           '2014-01-01T00:00:00.000000000', '2015-01-01T00:00:00.000000000'],
          dtype='datetime64[ns]')

  • y
    (y)
    float64
    5.665e+05 5.655e+05 ... 5.505e+05

    array([566500., 565500., 564500., 563500., 562500., 561500., 560500., 559500.,
           558500., 557500., 556500., 555500., 554500., 553500., 552500., 551500.,
           550500.])

  • x
    (x)
    float64
    2.305e+05 2.315e+05 ... 2.565e+05

    array([230500., 231500., 232500., 233500., 234500., 235500., 236500., 237500.,
           238500., 239500., 240500., 241500., 242500., 243500., 244500., 245500.,
           246500., 247500., 248500., 249500., 250500., 251500., 252500., 253500.,
           254500., 255500., 256500.])

  • dx
    ()
    float64
    1e+03

    array(1000.)

  • dy
    ()
    float64
    -1e+03

    array(-1000.)

• Attributes: (1)

  units :

  mm/d

To create the final recharge for the transient simulation, the steady state information needs to be concatenated to the transient recharge data. The steady state simulation will be run for one second. This is achieved by using the numpy Timedelta function, first creating a time delta of 1 second, which is assigned to the steady state recharge information. This dataset is then concatenated using the xarray function xarray.concat to the transient information and indicating that the dimension to join is “time”.

starttime = "2009-12-31"

# Add first steady-state
timedelta = np.timedelta64(1, "s")  # 1 second duration for initial steady-state
starttime_steady = np.datetime64(starttime) - timedelta
rch_ss = rch_ss.assign_coords(time=starttime_steady)

rch_ss_trans = xr.concat([rch_ss, rch_trans_yr], dim="time")
rch_ss_trans

<xarray.DataArray (y: 17, x: 27, time: 7)> Size: 13kB
array([[[0.00091255, 0.00191725, 0.00175232, ..., 0.00167949,
         0.00161827, 0.00226806],
        [0.0009093 , 0.00191589, 0.0017549 , ..., 0.001689  ,
         0.00161518, 0.00225167],
        [0.00090591, 0.00191248, 0.00175632, ..., 0.00169961,
         0.00161301, 0.00223808],
        ...,
        [0.00078183, 0.00158879, 0.00160428, ..., 0.00174276,
         0.00162122, 0.00221006],
        [0.00078091, 0.00160275, 0.0016166 , ..., 0.00174685,
         0.0016207 , 0.00219559],
        [0.00078071, 0.00161772, 0.00163142, ..., 0.00175276,
         0.00162407, 0.00218172]],

       [[0.000913  , 0.00193096, 0.00175832, ..., 0.00168658,
         0.00164151, 0.0022924 ],
        [0.0009098 , 0.00193016, 0.00176321, ..., 0.00169678,
         0.00163919, 0.00227892],
        [0.0009065 , 0.0019277 , 0.00176716, ..., 0.00170842,
         0.00163841, 0.00226807],
...
        [0.00085378, 0.00177083, 0.00186831, ..., 0.00174713,
         0.00169624, 0.00224585],
        [0.00084055, 0.0017666 , 0.00185661, ..., 0.00173329,
         0.00168655, 0.00223096],
        [0.00082746, 0.00176362, 0.00184691, ..., 0.00172136,
         0.0016792 , 0.00221743]],

       [[0.00098196, 0.00204444, 0.00188612, ..., 0.00182747,
         0.0019308 , 0.00249155],
        [0.00098031, 0.002041  , 0.00189853, ..., 0.00183236,
         0.00192603, 0.00248376],
        [0.00097932, 0.00203658, 0.00191231, ..., 0.00183771,
         0.0019212 , 0.00247603],
        ...,
        [0.00086102, 0.00178251, 0.00188156, ..., 0.00175411,
         0.00170712, 0.00224736],
        [0.00084771, 0.00177807, 0.00187044, ..., 0.0017413 ,
         0.00169771, 0.00223372],
        [0.0008352 , 0.00177411, 0.00186046, ..., 0.00173005,
         0.00169032, 0.00222133]]], shape=(17, 27, 7), dtype=float32)
Coordinates:
  * y        (y) float64 136B 5.665e+05 5.655e+05 ... 5.515e+05 5.505e+05
  * x        (x) float64 216B 2.305e+05 2.315e+05 ... 2.555e+05 2.565e+05
  * time     (time) datetime64[ns] 56B 2009-12-30T23:59:59 ... 2015-01-01
    dx       float64 8B 1e+03
    dy       float64 8B -1e+03
Attributes:
    units:    mm/d

xarray.DataArray

• y: 17
• x: 27
• time: 7

• 0.0009125 0.001917 0.001752 0.001906 ... 0.00173 0.00169 0.002221

  array([[[0.00091255, 0.00191725, 0.00175232, ..., 0.00167949,
           0.00161827, 0.00226806],
          [0.0009093 , 0.00191589, 0.0017549 , ..., 0.001689  ,
           0.00161518, 0.00225167],
          [0.00090591, 0.00191248, 0.00175632, ..., 0.00169961,
           0.00161301, 0.00223808],
          ...,
          [0.00078183, 0.00158879, 0.00160428, ..., 0.00174276,
           0.00162122, 0.00221006],
          [0.00078091, 0.00160275, 0.0016166 , ..., 0.00174685,
           0.0016207 , 0.00219559],
          [0.00078071, 0.00161772, 0.00163142, ..., 0.00175276,
           0.00162407, 0.00218172]],
  
         [[0.000913  , 0.00193096, 0.00175832, ..., 0.00168658,
           0.00164151, 0.0022924 ],
          [0.0009098 , 0.00193016, 0.00176321, ..., 0.00169678,
           0.00163919, 0.00227892],
          [0.0009065 , 0.0019277 , 0.00176716, ..., 0.00170842,
           0.00163841, 0.00226807],
  ...
          [0.00085378, 0.00177083, 0.00186831, ..., 0.00174713,
           0.00169624, 0.00224585],
          [0.00084055, 0.0017666 , 0.00185661, ..., 0.00173329,
           0.00168655, 0.00223096],
          [0.00082746, 0.00176362, 0.00184691, ..., 0.00172136,
           0.0016792 , 0.00221743]],
  
         [[0.00098196, 0.00204444, 0.00188612, ..., 0.00182747,
           0.0019308 , 0.00249155],
          [0.00098031, 0.002041  , 0.00189853, ..., 0.00183236,
           0.00192603, 0.00248376],
          [0.00097932, 0.00203658, 0.00191231, ..., 0.00183771,
           0.0019212 , 0.00247603],
          ...,
          [0.00086102, 0.00178251, 0.00188156, ..., 0.00175411,
           0.00170712, 0.00224736],
          [0.00084771, 0.00177807, 0.00187044, ..., 0.0017413 ,
           0.00169771, 0.00223372],
          [0.0008352 , 0.00177411, 0.00186046, ..., 0.00173005,
           0.00169032, 0.00222133]]], shape=(17, 27, 7), dtype=float32)

• Coordinates: (5)
  • y
    (y)
    float64
    5.665e+05 5.655e+05 ... 5.505e+05

    array([566500., 565500., 564500., 563500., 562500., 561500., 560500., 559500.,
           558500., 557500., 556500., 555500., 554500., 553500., 552500., 551500.,
           550500.])

  • x
    (x)
    float64
    2.305e+05 2.315e+05 ... 2.565e+05

    array([230500., 231500., 232500., 233500., 234500., 235500., 236500., 237500.,
           238500., 239500., 240500., 241500., 242500., 243500., 244500., 245500.,
           246500., 247500., 248500., 249500., 250500., 251500., 252500., 253500.,
           254500., 255500., 256500.])

  • time
    (time)
    datetime64[ns]
    2009-12-30T23:59:59 ... 2015-01-01

    array(['2009-12-30T23:59:59.000000000', '2010-01-01T00:00:00.000000000',
           '2011-01-01T00:00:00.000000000', '2012-01-01T00:00:00.000000000',
           '2013-01-01T00:00:00.000000000', '2014-01-01T00:00:00.000000000',
           '2015-01-01T00:00:00.000000000'], dtype='datetime64[ns]')

  • dx
    ()
    float64
    1e+03

    array(1000.)

  • dy
    ()
    float64
    -1e+03

    array(-1000.)

• Attributes: (1)

  units :

  mm/d

The data obtained from KNMI has different grid dimensions than the one considered in this example. To fix this, we’ll have to regrid the data to the model grid. xugrid has Regridder functionality that allows to regrid data with different methods. It is also possible to define the regridding method such as nearest, multilinear, mean, among others. In this case, mean was selected and the 2d template (like_2d) was used as reference, as this is the geometry to be considered in the model.

import xugrid as xu

regridder = xu.OverlapRegridder(rch_ss, like_2d, method="mean")
rch_ss_trans = regridder.regrid(rch_ss_trans)
rch_ss_trans

<xarray.DataArray (time: 7, y: 200, x: 500)> Size: 6MB
array([[[0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
         0.00083373, 0.00083373],
        [0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
         0.00083373, 0.00083373],
        [0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
         0.00083373, 0.00083373],
        ...,
        [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
         0.00088318, 0.00088318],
        [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
         0.00088318, 0.00088318],
        [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
         0.00088318, 0.00088318]],

       [[0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
         0.00163785, 0.00163785],
        [0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
         0.00163785, 0.00163785],
        [0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
         0.00163785, 0.00163785],
...
        [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
         0.00171221, 0.00171221],
        [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
         0.00171221, 0.00171221],
        [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
         0.00171221, 0.00171221]],

       [[0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
         0.00231468, 0.00231468],
        [0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
         0.00231468, 0.00231468],
        [0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
         0.00231468, 0.00231468],
        ...,
        [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
         0.0023817 , 0.0023817 ],
        [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
         0.0023817 , 0.0023817 ],
        [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
         0.0023817 , 0.0023817 ]]], shape=(7, 200, 500))
Coordinates:
  * time     (time) datetime64[ns] 56B 2009-12-30T23:59:59 ... 2015-01-01
  * y        (y) float64 2kB 5.64e+05 5.64e+05 5.639e+05 ... 5.59e+05 5.59e+05
  * x        (x) float64 4kB 2.375e+05 2.375e+05 2.376e+05 ... 2.5e+05 2.5e+05
    dx       float64 8B 25.0
    dy       float64 8B -25.0
Attributes:
    units:    mm/d

xarray.DataArray

• time: 7
• y: 200
• x: 500

• 0.0008994 0.0008994 0.0008994 0.0008994 ... 0.002382 0.002382 0.002382

  array([[[0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
           0.00083373, 0.00083373],
          [0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
           0.00083373, 0.00083373],
          [0.00089943, 0.00089943, 0.00089943, ..., 0.00083373,
           0.00083373, 0.00083373],
          ...,
          [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
           0.00088318, 0.00088318],
          [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
           0.00088318, 0.00088318],
          [0.00091826, 0.00091826, 0.00091826, ..., 0.00088318,
           0.00088318, 0.00088318]],
  
         [[0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
           0.00163785, 0.00163785],
          [0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
           0.00163785, 0.00163785],
          [0.00190719, 0.00190719, 0.00190719, ..., 0.00163785,
           0.00163785, 0.00163785],
  ...
          [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
           0.00171221, 0.00171221],
          [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
           0.00171221, 0.00171221],
          [0.00179237, 0.00179237, 0.00179237, ..., 0.00171221,
           0.00171221, 0.00171221]],
  
         [[0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
           0.00231468, 0.00231468],
          [0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
           0.00231468, 0.00231468],
          [0.00232221, 0.00232221, 0.00232221, ..., 0.00231468,
           0.00231468, 0.00231468],
          ...,
          [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
           0.0023817 , 0.0023817 ],
          [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
           0.0023817 , 0.0023817 ],
          [0.00242177, 0.00242177, 0.00242177, ..., 0.0023817 ,
           0.0023817 , 0.0023817 ]]], shape=(7, 200, 500))

• Coordinates: (5)
  • time
    (time)
    datetime64[ns]
    2009-12-30T23:59:59 ... 2015-01-01

    array(['2009-12-30T23:59:59.000000000', '2010-01-01T00:00:00.000000000',
           '2011-01-01T00:00:00.000000000', '2012-01-01T00:00:00.000000000',
           '2013-01-01T00:00:00.000000000', '2014-01-01T00:00:00.000000000',
           '2015-01-01T00:00:00.000000000'], dtype='datetime64[ns]')

  • y
    (y)
    float64
    5.64e+05 5.64e+05 ... 5.59e+05

    array([563987.5, 563962.5, 563937.5, 563912.5, 563887.5, 563862.5, 563837.5,
           563812.5, 563787.5, 563762.5, 563737.5, 563712.5, 563687.5, 563662.5,
           563637.5, 563612.5, 563587.5, 563562.5, 563537.5, 563512.5, 563487.5,
           563462.5, 563437.5, 563412.5, 563387.5, 563362.5, 563337.5, 563312.5,
           563287.5, 563262.5, 563237.5, 563212.5, 563187.5, 563162.5, 563137.5,
           563112.5, 563087.5, 563062.5, 563037.5, 563012.5, 562987.5, 562962.5,
           562937.5, 562912.5, 562887.5, 562862.5, 562837.5, 562812.5, 562787.5,
           562762.5, 562737.5, 562712.5, 562687.5, 562662.5, 562637.5, 562612.5,
           562587.5, 562562.5, 562537.5, 562512.5, 562487.5, 562462.5, 562437.5,
           562412.5, 562387.5, 562362.5, 562337.5, 562312.5, 562287.5, 562262.5,
           562237.5, 562212.5, 562187.5, 562162.5, 562137.5, 562112.5, 562087.5,
           562062.5, 562037.5, 562012.5, 561987.5, 561962.5, 561937.5, 561912.5,
           561887.5, 561862.5, 561837.5, 561812.5, 561787.5, 561762.5, 561737.5,
           561712.5, 561687.5, 561662.5, 561637.5, 561612.5, 561587.5, 561562.5,
           561537.5, 561512.5, 561487.5, 561462.5, 561437.5, 561412.5, 561387.5,
           561362.5, 561337.5, 561312.5, 561287.5, 561262.5, 561237.5, 561212.5,
           561187.5, 561162.5, 561137.5, 561112.5, 561087.5, 561062.5, 561037.5,
           561012.5, 560987.5, 560962.5, 560937.5, 560912.5, 560887.5, 560862.5,
           560837.5, 560812.5, 560787.5, 560762.5, 560737.5, 560712.5, 560687.5,
           560662.5, 560637.5, 560612.5, 560587.5, 560562.5, 560537.5, 560512.5,
           560487.5, 560462.5, 560437.5, 560412.5, 560387.5, 560362.5, 560337.5,
           560312.5, 560287.5, 560262.5, 560237.5, 560212.5, 560187.5, 560162.5,
           560137.5, 560112.5, 560087.5, 560062.5, 560037.5, 560012.5, 559987.5,
           559962.5, 559937.5, 559912.5, 559887.5, 559862.5, 559837.5, 559812.5,
           559787.5, 559762.5, 559737.5, 559712.5, 559687.5, 559662.5, 559637.5,
           559612.5, 559587.5, 559562.5, 559537.5, 559512.5, 559487.5, 559462.5,
           559437.5, 559412.5, 559387.5, 559362.5, 559337.5, 559312.5, 559287.5,
           559262.5, 559237.5, 559212.5, 559187.5, 559162.5, 559137.5, 559112.5,
           559087.5, 559062.5, 559037.5, 559012.5])

  • x
    (x)
    float64
    2.375e+05 2.375e+05 ... 2.5e+05

    array([237512.5, 237537.5, 237562.5, ..., 249937.5, 249962.5, 249987.5],
          shape=(500,))

  • dx
    ()
    float64
    25.0

    array(25.)

  • dy
    ()
    float64
    -25.0

    array(-25.)

• Attributes: (1)

  units :

  mm/d

The previously created recharge array is a 2D array that needs to be assigned to a 3D array. This is done using the xarray DataArray.where option, where the recharge values are applied to the cells where the idomain value is larger than zero (that is, the active cells) and for the uppermost active cell (indicated by the minimum layer number).

rch_total = rch_ss_trans.where(
    idomain["layer"] == idomain["layer"].where(idomain > 0).min("layer")
)
rch_total

<xarray.DataArray (time: 7, y: 200, x: 500, layer: 13)> Size: 73MB
array([[[[       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
         ...,
         [0.00083373,        nan,        nan, ...,        nan,
                 nan,        nan],
         [0.00083373,        nan,        nan, ...,        nan,
                 nan,        nan],
         [0.00083373,        nan,        nan, ...,        nan,
                 nan,        nan]],

        [[       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.00089943, ...,        nan,
                 nan,        nan],
...
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan]],

        [[0.00242177,        nan,        nan, ...,        nan,
                 nan,        nan],
         [0.00242177,        nan,        nan, ...,        nan,
                 nan,        nan],
         [0.00242177,        nan,        nan, ...,        nan,
                 nan,        nan],
         ...,
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan],
         [       nan,        nan, 0.0023817 , ...,        nan,
                 nan,        nan]]]], shape=(7, 200, 500, 13))
Coordinates:
  * time     (time) datetime64[ns] 56B 2009-12-30T23:59:59 ... 2015-01-01
  * y        (y) float64 2kB 5.64e+05 5.64e+05 5.639e+05 ... 5.59e+05 5.59e+05
  * x        (x) float64 4kB 2.375e+05 2.375e+05 2.376e+05 ... 2.5e+05 2.5e+05
  * layer    (layer) int32 52B 1 2 3 4 5 6 7 8 9 10 11 12 13
    dx       float64 8B 25.0
    dy       float64 8B -25.0
Attributes:
    units:    mm/d

xarray.DataArray

• time: 7
• y: 200
• x: 500
• layer: 13

• nan nan 0.0008994 nan nan nan nan nan ... nan nan nan nan nan nan nan

  array([[[[       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
           ...,
           [0.00083373,        nan,        nan, ...,        nan,
                   nan,        nan],
           [0.00083373,        nan,        nan, ...,        nan,
                   nan,        nan],
           [0.00083373,        nan,        nan, ...,        nan,
                   nan,        nan]],
  
          [[       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.00089943, ...,        nan,
                   nan,        nan],
  ...
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan]],
  
          [[0.00242177,        nan,        nan, ...,        nan,
                   nan,        nan],
           [0.00242177,        nan,        nan, ...,        nan,
                   nan,        nan],
           [0.00242177,        nan,        nan, ...,        nan,
                   nan,        nan],
           ...,
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan],
           [       nan,        nan, 0.0023817 , ...,        nan,
                   nan,        nan]]]], shape=(7, 200, 500, 13))

• Coordinates: (6)
  • time
    (time)
    datetime64[ns]
    2009-12-30T23:59:59 ... 2015-01-01

    array(['2009-12-30T23:59:59.000000000', '2010-01-01T00:00:00.000000000',
           '2011-01-01T00:00:00.000000000', '2012-01-01T00:00:00.000000000',
           '2013-01-01T00:00:00.000000000', '2014-01-01T00:00:00.000000000',
           '2015-01-01T00:00:00.000000000'], dtype='datetime64[ns]')

  • y
    (y)
    float64
    5.64e+05 5.64e+05 ... 5.59e+05

    array([563987.5, 563962.5, 563937.5, 563912.5, 563887.5, 563862.5, 563837.5,
           563812.5, 563787.5, 563762.5, 563737.5, 563712.5, 563687.5, 563662.5,
           563637.5, 563612.5, 563587.5, 563562.5, 563537.5, 563512.5, 563487.5,
           563462.5, 563437.5, 563412.5, 563387.5, 563362.5, 563337.5, 563312.5,
           563287.5, 563262.5, 563237.5, 563212.5, 563187.5, 563162.5, 563137.5,
           563112.5, 563087.5, 563062.5, 563037.5, 563012.5, 562987.5, 562962.5,
           562937.5, 562912.5, 562887.5, 562862.5, 562837.5, 562812.5, 562787.5,
           562762.5, 562737.5, 562712.5, 562687.5, 562662.5, 562637.5, 562612.5,
           562587.5, 562562.5, 562537.5, 562512.5, 562487.5, 562462.5, 562437.5,
           562412.5, 562387.5, 562362.5, 562337.5, 562312.5, 562287.5, 562262.5,
           562237.5, 562212.5, 562187.5, 562162.5, 562137.5, 562112.5, 562087.5,
           562062.5, 562037.5, 562012.5, 561987.5, 561962.5, 561937.5, 561912.5,
           561887.5, 561862.5, 561837.5, 561812.5, 561787.5, 561762.5, 561737.5,
           561712.5, 561687.5, 561662.5, 561637.5, 561612.5, 561587.5, 561562.5,
           561537.5, 561512.5, 561487.5, 561462.5, 561437.5, 561412.5, 561387.5,
           561362.5, 561337.5, 561312.5, 561287.5, 561262.5, 561237.5, 561212.5,
           561187.5, 561162.5, 561137.5, 561112.5, 561087.5, 561062.5, 561037.5,
           561012.5, 560987.5, 560962.5, 560937.5, 560912.5, 560887.5, 560862.5,
           560837.5, 560812.5, 560787.5, 560762.5, 560737.5, 560712.5, 560687.5,
           560662.5, 560637.5, 560612.5, 560587.5, 560562.5, 560537.5, 560512.5,
           560487.5, 560462.5, 560437.5, 560412.5, 560387.5, 560362.5, 560337.5,
           560312.5, 560287.5, 560262.5, 560237.5, 560212.5, 560187.5, 560162.5,
           560137.5, 560112.5, 560087.5, 560062.5, 560037.5, 560012.5, 559987.5,
           559962.5, 559937.5, 559912.5, 559887.5, 559862.5, 559837.5, 559812.5,
           559787.5, 559762.5, 559737.5, 559712.5, 559687.5, 559662.5, 559637.5,
           559612.5, 559587.5, 559562.5, 559537.5, 559512.5, 559487.5, 559462.5,
           559437.5, 559412.5, 559387.5, 559362.5, 559337.5, 559312.5, 559287.5,
           559262.5, 559237.5, 559212.5, 559187.5, 559162.5, 559137.5, 559112.5,
           559087.5, 559062.5, 559037.5, 559012.5])

  • x
    (x)
    float64
    2.375e+05 2.375e+05 ... 2.5e+05

    array([237512.5, 237537.5, 237562.5, ..., 249937.5, 249962.5, 249987.5],
          shape=(500,))

  • layer
    (layer)
    int32
    1 2 3 4 5 6 7 8 9 10 11 12 13

    array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13], dtype=int32)

  • dx
    ()
    float64
    25.0

    array(25.)

  • dy
    ()
    float64
    -25.0

    array(-25.)

• Attributes: (1)

  units :

  mm/d

Finally, transposing the array dimensions using DataArray.transpose so they are in the correct order.

rch_total = rch_total.transpose("time", "layer", "y", "x")
rch_total

fig, ax = plt.subplots()
rch_total.isel(layer=2, time=6).plot.imshow(ax=ax)

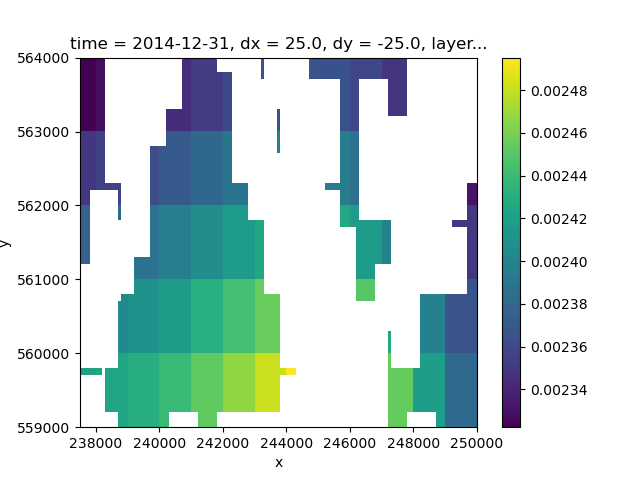
<matplotlib.image.AxesImage object at 0x000001466DA08190>

Adding information to the RCH package

The information for the RCH package is added with the function imod.mf6.Recharge. It is required to insert the recharge flux rate, and it is optional to include the print_input, print_flows and save_flows information.

gwf_model["rch"] = imod.mf6.Recharge(rch_total)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 413, in <module>
    gwf_model["rch"] = imod.mf6.Recharge(rch_total)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Recharge package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 413, in <module>
    gwf_model["rch"] = imod.mf6.Recharge(rch_total)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 170, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 175, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Recharge...'
Arguments: ()

Drainage package - DRN

The drain package is used to simulate features that remove water from the aquifer, such as agricultural drains or springs. This occurs at a rate proportional to the head difference between the head in the aquifer and the drain elevation (the head in the aquifer has to be above that elevation). The conductance is the proportionality constant.

Import drainage information

drainage = imod.data.hondsrug_drainage()

pipe_cond = drainage["conductance"]
pipe_elev = drainage["elevation"]

pipe_cond

<xarray.DataArray 'conductance' (layer: 4, y: 200, x: 500)> Size: 2MB
[400000 values with dtype=float32]
Coordinates:
  * layer    (layer) int32 16B 1 3 5 6
  * y        (y) float64 2kB 5.64e+05 5.64e+05 5.639e+05 ... 5.59e+05 5.59e+05
  * x        (x) float64 4kB 2.375e+05 2.375e+05 2.376e+05 ... 2.5e+05 2.5e+05
    dx       float64 8B ...
    dy       float64 8B ...

xarray.DataArray

'conductance'

• layer: 4
• y: 200
• x: 500

• ...

  [400000 values with dtype=float32]

• Coordinates: (5)
  • layer
    (layer)
    int32
    1 3 5 6

    array([1, 3, 5, 6], dtype=int32)

  • y
    (y)
    float64
    5.64e+05 5.64e+05 ... 5.59e+05

    array([563987.5, 563962.5, 563937.5, 563912.5, 563887.5, 563862.5, 563837.5,
           563812.5, 563787.5, 563762.5, 563737.5, 563712.5, 563687.5, 563662.5,
           563637.5, 563612.5, 563587.5, 563562.5, 563537.5, 563512.5, 563487.5,
           563462.5, 563437.5, 563412.5, 563387.5, 563362.5, 563337.5, 563312.5,
           563287.5, 563262.5, 563237.5, 563212.5, 563187.5, 563162.5, 563137.5,
           563112.5, 563087.5, 563062.5, 563037.5, 563012.5, 562987.5, 562962.5,
           562937.5, 562912.5, 562887.5, 562862.5, 562837.5, 562812.5, 562787.5,
           562762.5, 562737.5, 562712.5, 562687.5, 562662.5, 562637.5, 562612.5,
           562587.5, 562562.5, 562537.5, 562512.5, 562487.5, 562462.5, 562437.5,
           562412.5, 562387.5, 562362.5, 562337.5, 562312.5, 562287.5, 562262.5,
           562237.5, 562212.5, 562187.5, 562162.5, 562137.5, 562112.5, 562087.5,
           562062.5, 562037.5, 562012.5, 561987.5, 561962.5, 561937.5, 561912.5,
           561887.5, 561862.5, 561837.5, 561812.5, 561787.5, 561762.5, 561737.5,
           561712.5, 561687.5, 561662.5, 561637.5, 561612.5, 561587.5, 561562.5,
           561537.5, 561512.5, 561487.5, 561462.5, 561437.5, 561412.5, 561387.5,
           561362.5, 561337.5, 561312.5, 561287.5, 561262.5, 561237.5, 561212.5,
           561187.5, 561162.5, 561137.5, 561112.5, 561087.5, 561062.5, 561037.5,
           561012.5, 560987.5, 560962.5, 560937.5, 560912.5, 560887.5, 560862.5,
           560837.5, 560812.5, 560787.5, 560762.5, 560737.5, 560712.5, 560687.5,
           560662.5, 560637.5, 560612.5, 560587.5, 560562.5, 560537.5, 560512.5,
           560487.5, 560462.5, 560437.5, 560412.5, 560387.5, 560362.5, 560337.5,
           560312.5, 560287.5, 560262.5, 560237.5, 560212.5, 560187.5, 560162.5,
           560137.5, 560112.5, 560087.5, 560062.5, 560037.5, 560012.5, 559987.5,
           559962.5, 559937.5, 559912.5, 559887.5, 559862.5, 559837.5, 559812.5,
           559787.5, 559762.5, 559737.5, 559712.5, 559687.5, 559662.5, 559637.5,
           559612.5, 559587.5, 559562.5, 559537.5, 559512.5, 559487.5, 559462.5,
           559437.5, 559412.5, 559387.5, 559362.5, 559337.5, 559312.5, 559287.5,
           559262.5, 559237.5, 559212.5, 559187.5, 559162.5, 559137.5, 559112.5,
           559087.5, 559062.5, 559037.5, 559012.5])

  • x
    (x)
    float64
    2.375e+05 2.375e+05 ... 2.5e+05

    array([237512.5, 237537.5, 237562.5, ..., 249937.5, 249962.5, 249987.5],
          shape=(500,))

  • dx
    ()
    float64
    ...

    [1 values with dtype=float64]

  • dy
    ()
    float64
    ...

    [1 values with dtype=float64]

Adding information to the DRN package

To add the information to the DRN package within the gwf_model variable, the imod.mf6.Drainage. function is used. It is required to add the previously created arrays for the drain elevation and the drain conductance. It is optional to insert the information for print_input, print_flows and save_flows which are set to False by default.

gwf_model["drn-pipe"] = imod.mf6.Drainage(conductance=pipe_cond, elevation=pipe_elev)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 448, in <module>
    gwf_model["drn-pipe"] = imod.mf6.Drainage(conductance=pipe_cond, elevation=pipe_elev)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Drainage package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 448, in <module>
    gwf_model["drn-pipe"] = imod.mf6.Drainage(conductance=pipe_cond, elevation=pipe_elev)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\drn.py", line 165, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\drn.py", line 170, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Drainage...'
Arguments: ()

River package - RIV

This package simulates the effects of flow between surface-water features and groundwater systems.

Import river information

river = imod.data.hondsrug_river()
riv_cond = river["conductance"]
riv_stage = river["stage"]
riv_bot = river["bottom"]

Adding information to the RIV package

The data is assigned to the gwf_model variable by using imod.mf6.River, based on the previously imported conductance, stage and bottom arrays.

gwf_model["riv"] = imod.mf6.River(
    conductance=riv_cond, stage=riv_stage, bottom_elevation=riv_bot
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 473, in <module>
    gwf_model["riv"] = imod.mf6.River(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the River package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 473, in <module>
    gwf_model["riv"] = imod.mf6.River(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\riv.py", line 288, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\riv.py", line 294, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object River...'
Arguments: ()

Storage package - STO

When the STO Package is included in a model, storage changes will be calculated, and thus, the model will be transient.

ss = 0.0003
layer = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13])
sy = xr.DataArray(
    [0.16, 0.16, 0.16, 0.16, 0.15, 0.15, 0.15, 0.15, 0.14, 0.14, 0.14, 0.14, 0.14],
    {"layer": layer},
    ("layer",),
)
times_sto = np.array(
    [
        "2009-12-30T23:59:59.00",
        "2009-12-31T00:00:00.00",
        "2010-12-31T00:00:00.00",
        "2011-12-31T00:00:00.00",
        "2012-12-31T00:00:00.00",
        "2013-12-31T00:00:00.00",
        "2014-12-31T00:00:00.00",
    ],
    dtype="datetime64[ns]",
)

transient = xr.DataArray(
    [False, True, True, True, True, True, True], {"time": times_sto}, ("time",)
)

Adding information to the STO package

The data is assigned to the gwf_model variable by using imod.mf6.SpecificStorage. It is necessary to indicate the values of specific storage, specific yield and if the layers are convertible.

gwf_model["sto"] = imod.mf6.SpecificStorage(
    specific_storage=ss,
    specific_yield=sy,
    transient=transient,
    convertible=0,
    save_flows=True,
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 517, in <module>
    gwf_model["sto"] = imod.mf6.SpecificStorage(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SpecificStorage package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 517, in <module>
    gwf_model["sto"] = imod.mf6.SpecificStorage(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\sto.py", line 187, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()

Output Control package - OC

This package determines how and when heads are printed to the listing file and/or written to a separate binary output file

Adding information to the OC package

The function imod.mf6.OutputControl is used to store the information for this package. It is possible to indicate if the heads and budget information is saved at the end of each stress period (last), for all timesteps a stress period (all), or at the start of a stress period (first)

gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 543, in <module>
    gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 543, in <module>
    gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()

Model simulation

In MODFLOW 6, the concept of “model” is that part of the program that solves a hydrologic process. MODFLOW 6 documentation supports one type of model: the GWF Model. It is possible within the MODFLOW 6 framewotk to solve multiple, tightly coupled, numerical models in a single system of equation, which may be multiple models of the same type or of different types.

The previously created gwf_model variable now contains the information from all the variables.

gwf_model

GroundwaterFlowModel(
    listing_file=None,
    print_input=False,
    print_flows=False,
    save_flows=False,
    newton=False,
    under_relaxation=False,
){
    'dis': StructuredDiscretization,
    'npf': NodePropertyFlow,
    'ic': InitialConditions,
    'chd': ConstantHead,
    'rch': Recharge,
    'drn-pipe': Drainage,
    'riv': River,
    'sto': SpecificStorage,
    'oc': OutputControl,
}

Attach the model information to a simulation

The function imod.mf6.Modflow6Simulation allows to assign models to a simulation (in this case, the gwf_model).

simulation = imod.mf6.Modflow6Simulation("mf6-mipwa2-example")
simulation["GWF_1"] = gwf_model

Solver settings

The solver settings are indicated using imod.mf6.Solution. If the values are not indicated manually, the defaults values will be considered.

simulation["solver"] = imod.mf6.Solution(
    modelnames=["GWF_1"],
    print_option="summary",
    outer_dvclose=1.0e-4,
    outer_maximum=500,
    under_relaxation=None,
    inner_dvclose=1.0e-4,
    inner_rclose=0.001,
    inner_maximum=100,
    linear_acceleration="cg",
    scaling_method=None,
    reordering_method=None,
    relaxation_factor=0.97,
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 580, in <module>
    simulation["solver"] = imod.mf6.Solution(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Solution package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 580, in <module>
    simulation["solver"] = imod.mf6.Solution(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ims.py", line 451, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Solution...'
Arguments: ()

Assign time discretization

The time discretization of this model is 6 years.

simulation.create_time_discretization(
    additional_times=["2009-12-30T23:59:59.000000000", "2015-12-31T00:00:00.000000000"]
)

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
    mem_last, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 601, in <module>
    simulation.create_time_discretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.create_time_discretization for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
    mem_last, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 601, in <module>
    simulation.create_time_discretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
    self["time_discretization"] = imod.mf6.TimeDiscretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the TimeDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
    mem_last, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 601, in <module>
    simulation.create_time_discretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
    self["time_discretization"] = imod.mf6.TimeDiscretization(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\timedis.py", line 74, in __init__
    self._validate_init_schemata(validate)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
    validate_with_error_message(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
    errors = validate_func(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object TimeDiscretization...'
Arguments: ()

Run the model

Note

The following lines assume the mf6 executable is available on your PATH. The MODFLOW 6 examples introduction shortly describes how to add it to yours.

modeldir = imod.util.temporary_directory()
simulation.write(modeldir, binary=False)
simulation.run()

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.write for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
    option_errors = self._validate_options(self._init_schemata)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 175, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\drn.py", line 170, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Drainage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\riv.py", line 294, in _validate
    errors = super()._validate(schemata, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object River...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
    model_status_info = self.validate(modelname, validate_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
    return super().validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
    pkg_errors = pkg._validate(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
    super()._write(pkgname, globaltimes, write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
    super()._write(pkgname, globaltimes, write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
    super()._write(pkgname, globaltimes, write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Drainage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
    super()._write(pkgname, globaltimes, write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object River...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
    value._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
    pkg._write(
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
    super()._write(pkgname, globaltimes, write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
    mem_body, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 616, in <module>
    simulation.write(modeldir, binary=False)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
    return_value = fun(*args, **kwargs)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
    value._write(key, globaltimes, pkg_write_context)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
    mem_last, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 617, in <module>
    simulation.run()
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.run for object Modflow6Simulation...'
Arguments: ()

Results visualization

The next section indicated how to visualize the model results.

Import heads results

The heads results are imported using imod.mf6.open_hds. on the background.

hds = simulation.open_head()

--- Logging error ---
Traceback (most recent call last):
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
    stream.write(msg + self.terminator)
    ~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
    sys.exit(main())
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
    return make_mode.run_make_mode(argv[1:])
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
    return make.run_generic_build(builder_name)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
    return build_main(args + self.opts)
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
    app = Sphinx(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
    self._init_builder()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
    self.events.emit('builder-inited')
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
    results.append(listener.handler(self._app, *args))
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
    ) = generate_dir_rst(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
    results = parallel(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
    p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
    output_blocks, time_elapsed = execute_script(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
    execute_code_block(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
    is_last_expr, mem_max = _exec_and_get_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
    mem_max, _ = call_memory(
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
    return 0.0, func()
  File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
    exec(self.code, self.fake_main.__dict__)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\hondsrug.py", line 632, in <module>
    hds = simulation.open_head()
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
    logger.log(loglevel=start_level, message=start_message, additional_depth=2)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
    self.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
    self.instance.info(message, additional_depth)
  File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
    self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_head for object Modflow6Simulation...'
Arguments: ()

We can plot the data of an individual layer as follows

fig, ax = plt.subplots()
hds.sel(layer=3).isel(time=3).plot(ax=ax)

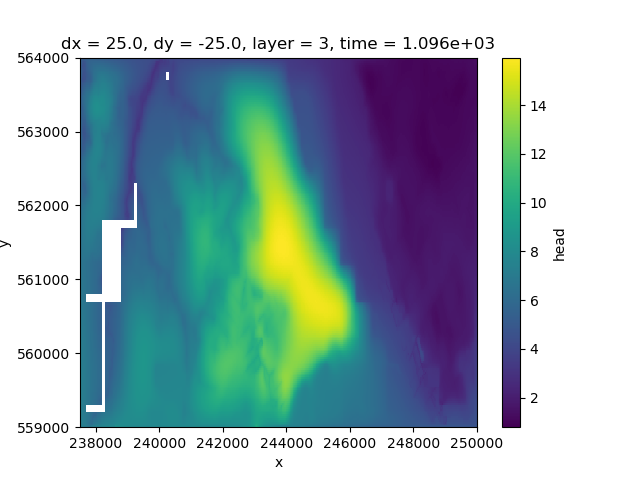
<matplotlib.collections.QuadMesh object at 0x000001466D221A90>

As you can see layer 3 has some missing cells in the west Whereas layer 4 only contains active cells in the eastern peatland area

fig, ax = plt.subplots()
hds.sel(layer=4).isel(time=3).plot(ax=ax)

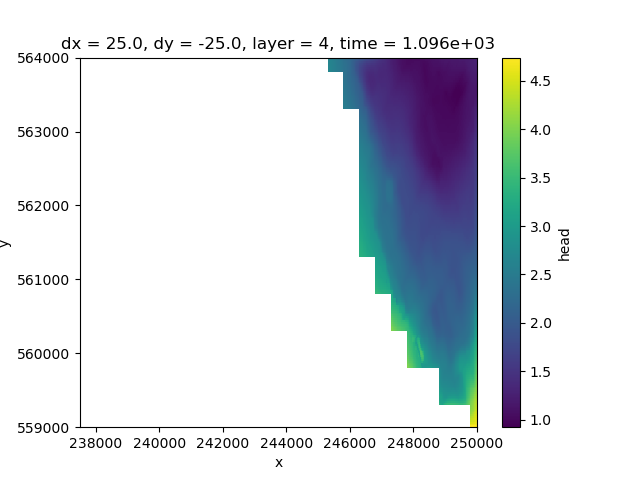
<matplotlib.collections.QuadMesh object at 0x000001464145B250>

Layer 5 contains more data towards the west, but has no active cells in the centre.

fig, ax = plt.subplots()
hds.sel(layer=5).isel(time=3).plot(ax=ax)

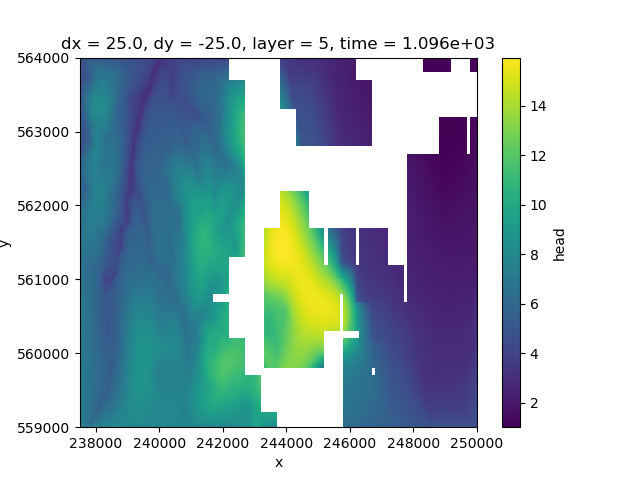
<matplotlib.collections.QuadMesh object at 0x0000014645BCBB10>

As you can see the data is individual layers have lots of inactive in different places.

It is difficult for this model to get a good idea what is happening across the area based on 1 layer alone. Luckily xarray allows us to compute the mean across a selection of layers and plot this.

By first selecting 3 layers with sel`, and then computing the mean across the layer dimension with mean(dim="layer").

fig, ax = plt.subplots()
hds.sel(layer=slice(3, 5)).mean(dim="layer").isel(time=3).plot(ax=ax)

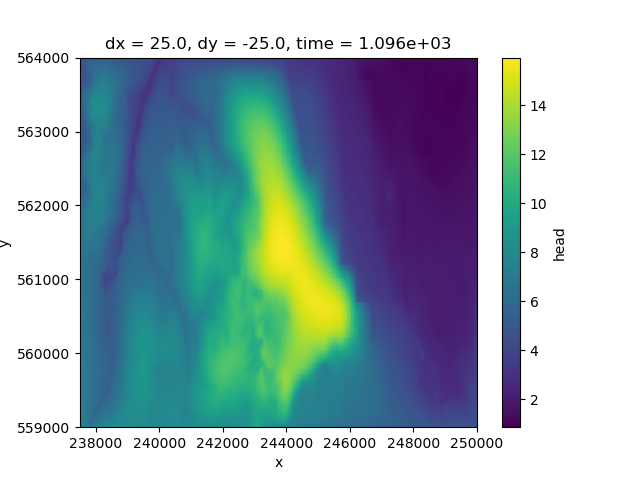
<matplotlib.collections.QuadMesh object at 0x000001464009FC50>

Assign dates to head

MODFLOW 6 has no concept of a calendar, so the output is not labelled only in terms of “time since start” in floating point numbers. For this model the time unit is days and we can assign a date coordinate as follows:

starttime = pd.to_datetime("2000-01-01")
timedelta = pd.to_timedelta(hds["time"], "D")
hds = hds.assign_coords(time=starttime + timedelta)

Extract head at points

A typical operation is to extract simulated heads at point locations to compare them with measurements. In this example, we select the heads at two points:

x = [240_000.0, 244_000.0]
y = [560_000.0, 562_000.0]
selection = imod.select.points_values(hds, x=x, y=y)

The result can be converted into a pandas dataframe for timeseries analysis, or written to a variety of tabular file formats.

dataframe = selection.to_dataframe().reset_index()
dataframe = dataframe.rename(columns={"index": "id"})
dataframe

	time	layer	id	x	y	dx	dy	head
0	2000-01-01 00:00:01.000000002	1	0	240012.5	560012.5	25.0	-25.0	NaN
1	2000-01-01 00:00:01.000000002	1	1	244012.5	562012.5	25.0	-25.0	10.534013
2	2000-01-01 00:00:01.000000002	2	0	240012.5	560012.5	25.0	-25.0	NaN
3	2000-01-01 00:00:01.000000002	2	1	244012.5	562012.5	25.0	-25.0	NaN
4	2000-01-01 00:00:01.000000002	3	0	240012.5	560012.5	25.0	-25.0	7.682111
...	...	...	...	...	...	...	...	...
333	2005-12-31 00:00:01.000000002	11	1	244012.5	562012.5	25.0	-25.0	4.787371
334	2005-12-31 00:00:01.000000002	12	0	240012.5	560012.5	25.0	-25.0	NaN
335	2005-12-31 00:00:01.000000002	12	1	244012.5	562012.5	25.0	-25.0	NaN
336	2005-12-31 00:00:01.000000002	13	0	240012.5	560012.5	25.0	-25.0	7.498576
337	2005-12-31 00:00:01.000000002	13	1	244012.5	562012.5	25.0	-25.0	4.787359

338 rows × 8 columns