Note
Go to the end to download the full example code.
1D Solute Transport Benchmarks#
This example is taken from the MODFLOW 6 Examples, number 35.
As explained there, the setup is a simple 1d homogeneous aquifer with a steady state flow field of constant velocity. The benchmark consists of four transport problems that are modeled using this flow field. Here we have modeled these four transport problems as a single simulation with multiple species. In all cases the initial concentration in the domain is zero, but water entering the domain has a concentration of one:
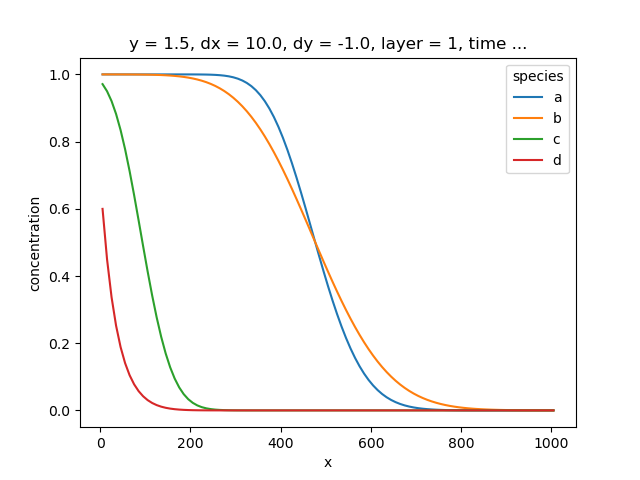
species a is transported with zero diffusion or dispersion and the concentration distribution should show a sharp front, but due to the numerical method we see some smearing, which is expected.
species b has a sizeable dispersivity and hence shows more smearing than species a but the same centre of mass.
Species c has linear sorption and therefore the concentration doesn’t enter the domain as far as species a or species b, but the front of the solute plume has the same overall shape as for species a or species b.
Species d has linear sorption and first order decay, and this changes the shape of the front of the solute plume.
import numpy as np
import pandas as pd
import xarray as xr
import imod
def create_transport_model(flowmodel, speciesname, dispersivity, retardation, decay):
"""
Function to create a transport model, as we intend to create four similar
transport models.
Parameters
----------
flowmodel: GroundwaterFlowModel
speciesname: str
dispersivity: float
retardation: float
decay: float
Returns
-------
transportmodel: GroundwaterTransportModel
"""
rhobulk = 1150.0
porosity = 0.25
tpt_model = imod.mf6.GroundwaterTransportModel()
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
flowmodel, speciesname, save_flows=True
)
tpt_model["adv"] = imod.mf6.AdvectionUpstream()
tpt_model["dsp"] = imod.mf6.Dispersion(
diffusion_coefficient=0.0,
longitudinal_horizontal=dispersivity,
transversal_horizontal1=0.0,
xt3d_off=False,
xt3d_rhs=False,
)
# Compute the sorption coefficient based on the desired retardation factor
# and the bulk density. Because of this, the exact value of bulk density
# does not matter for the solution.
if retardation != 1.0:
sorption = "linear"
kd = (retardation - 1.0) * porosity / rhobulk
else:
sorption = None
kd = 1.0
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
porosity=porosity,
decay=decay,
decay_sorbed=decay,
bulk_density=rhobulk,
distcoef=kd,
first_order_decay=True,
sorption=sorption,
)
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
tpt_model["oc"] = imod.mf6.OutputControl(
save_concentration="all", save_budget="last"
)
tpt_model["dis"] = flowmodel["dis"]
return tpt_model
Create the spatial discretization.
nlay = 1
nrow = 2
ncol = 101
dx = 10.0
xmin = 0.0
xmax = dx * ncol
layer = [1]
y = [1.5, 0.5]
x = np.arange(xmin, xmax, dx) + 0.5 * dx
grid_dims = ("layer", "y", "x")
grid_coords = {"layer": layer, "y": y, "x": x}
grid_shape = (nlay, nrow, ncol)
grid = xr.DataArray(np.ones(grid_shape, dtype=int), coords=grid_coords, dims=grid_dims)
bottom = xr.full_like(grid, -1.0, dtype=float)
gwf_model = imod.mf6.GroundwaterFlowModel()
gwf_model["ic"] = imod.mf6.InitialConditions(0.0)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 117, in <module>
gwf_model = imod.mf6.GroundwaterFlowModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterFlowModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 117, in <module>
gwf_model = imod.mf6.GroundwaterFlowModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 120, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 118, in <module>
gwf_model["ic"] = imod.mf6.InitialConditions(0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 118, in <module>
gwf_model["ic"] = imod.mf6.InitialConditions(0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
Create the input for a constant head boundary and its associated concentration.
constant_head = xr.full_like(grid, np.nan, dtype=float)
constant_head[..., 0] = 60.0
constant_head[..., 100] = 0.0
constant_conc = xr.full_like(grid, np.nan, dtype=float)
constant_conc[..., 0] = 1.0
constant_conc[..., 100] = 0.0
constant_conc = constant_conc.expand_dims(
species=["species_a", "species_b", "species_c", "species_d"]
)
gwf_model["chd"] = imod.mf6.ConstantHead(constant_head, constant_conc)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 133, in <module>
gwf_model["chd"] = imod.mf6.ConstantHead(constant_head, constant_conc)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantHead package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 133, in <module>
gwf_model["chd"] = imod.mf6.ConstantHead(constant_head, constant_conc)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 152, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
Add other flow packages.
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
icelltype=1,
k=xr.full_like(grid, 1.0, dtype=float),
variable_vertical_conductance=True,
dewatered=True,
perched=True,
)
gwf_model["dis"] = imod.mf6.StructuredDiscretization(
top=0.0,
bottom=bottom,
idomain=grid,
)
gwf_model["oc"] = imod.mf6.OutputControl(save_head="all", save_budget="all")
gwf_model["sto"] = imod.mf6.SpecificStorage(
specific_storage=1.0e-5,
specific_yield=0.15,
transient=False,
convertible=0,
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 138, in <module>
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the NodePropertyFlow package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 138, in <module>
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 423, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 145, in <module>
gwf_model["dis"] = imod.mf6.StructuredDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the StructuredDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 145, in <module>
gwf_model["dis"] = imod.mf6.StructuredDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 125, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 150, in <module>
gwf_model["oc"] = imod.mf6.OutputControl(save_head="all", save_budget="all")
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 150, in <module>
gwf_model["oc"] = imod.mf6.OutputControl(save_head="all", save_budget="all")
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 151, in <module>
gwf_model["sto"] = imod.mf6.SpecificStorage(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SpecificStorage package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 151, in <module>
gwf_model["sto"] = imod.mf6.SpecificStorage(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\sto.py", line 187, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
Create the simulation.
simulation = imod.mf6.Modflow6Simulation("1d_tpt_benchmark")
simulation["flow"] = gwf_model
Add four transport simulations, and setup the solver flow and transport.
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
simulation["flow_solver"] = imod.mf6.Solution(
modelnames=["flow"],
print_option="summary",
outer_dvclose=1.0e-4,
outer_maximum=500,
under_relaxation=None,
inner_dvclose=1.0e-4,
inner_rclose=0.001,
inner_maximum=100,
linear_acceleration="bicgstab",
scaling_method=None,
reordering_method=None,
relaxation_factor=0.97,
)
simulation["transport_solver"] = imod.mf6.Solution(
modelnames=["tpt_a", "tpt_b", "tpt_c", "tpt_d"],
print_option="summary",
outer_dvclose=1.0e-4,
outer_maximum=500,
under_relaxation=None,
inner_dvclose=1.0e-4,
inner_rclose=0.001,
inner_maximum=100,
linear_acceleration="bicgstab",
scaling_method=None,
reordering_method=None,
relaxation_factor=0.97,
)
duration = pd.to_timedelta("2000d")
start = pd.to_datetime("2000-01-01")
simulation.create_time_discretization(additional_times=[start, start + duration])
simulation["time_discretization"]["n_timesteps"] = 100
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SourceSinkMixing package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 61, in create_transport_model
tpt_model["adv"] = imod.mf6.AdvectionUpstream()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\adv.py", line 43, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Dispersion package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 181, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the MobileStorageTransfer package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\mst.py", line 134, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 166, in <module>
simulation["tpt_a"] = create_transport_model(gwf_model, "species_a", 0.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SourceSinkMixing package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 61, in create_transport_model
tpt_model["adv"] = imod.mf6.AdvectionUpstream()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\adv.py", line 43, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Dispersion package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 181, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the MobileStorageTransfer package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\mst.py", line 134, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 167, in <module>
simulation["tpt_b"] = create_transport_model(gwf_model, "species_b", 10.0, 1.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SourceSinkMixing package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 61, in create_transport_model
tpt_model["adv"] = imod.mf6.AdvectionUpstream()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\adv.py", line 43, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Dispersion package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 181, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the MobileStorageTransfer package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\mst.py", line 134, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 168, in <module>
simulation["tpt_c"] = create_transport_model(gwf_model, "species_c", 10.0, 5.0, 0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 57, in create_transport_model
tpt_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SourceSinkMixing package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 58, in create_transport_model
tpt_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 61, in create_transport_model
tpt_model["adv"] = imod.mf6.AdvectionUpstream()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\adv.py", line 43, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Dispersion package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 62, in create_transport_model
tpt_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 181, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the MobileStorageTransfer package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 80, in create_transport_model
tpt_model["mst"] = imod.mf6.MobileStorageTransfer(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\mst.py", line 134, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 90, in create_transport_model
tpt_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 169, in <module>
simulation["tpt_d"] = create_transport_model(gwf_model, "species_d", 10.0, 5.0, 0.002)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 91, in create_transport_model
tpt_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 171, in <module>
simulation["flow_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Solution package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 171, in <module>
simulation["flow_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ims.py", line 451, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 185, in <module>
simulation["transport_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Solution package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 185, in <module>
simulation["transport_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ims.py", line 451, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Solution...'
Arguments: ()
C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py:200: Pandas4Warning: 'd' is deprecated and will be removed in a future version. Please use 'D' instead of 'd'.
duration = pd.to_timedelta("2000d")
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 202, in <module>
simulation.create_time_discretization(additional_times=[start, start + duration])
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.create_time_discretization for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 202, in <module>
simulation.create_time_discretization(additional_times=[start, start + duration])
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
self["time_discretization"] = imod.mf6.TimeDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the TimeDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 202, in <module>
simulation.create_time_discretization(additional_times=[start, start + duration])
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
self["time_discretization"] = imod.mf6.TimeDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\timedis.py", line 74, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object TimeDiscretization...'
Arguments: ()
Run the simulation.
modeldir = imod.util.temporary_directory()
simulation.write(modeldir, binary=False)
simulation.run()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.write for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dis.py", line 168, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionUpstream...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object StructuredDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 208, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 209, in <module>
simulation.run()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.run for object Modflow6Simulation...'
Arguments: ()
Open the concentration results and store them in a single DataArray.
concentration = simulation.open_concentration(species_ls=["a", "b", "c", "d"])
mass_budgets = simulation.open_transport_budget(species_ls=["a", "b", "c", "d"])
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 214, in <module>
concentration = simulation.open_concentration(species_ls=["a", "b", "c", "d"])
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_concentration for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\example_1d_transport.py", line 215, in <module>
mass_budgets = simulation.open_transport_budget(species_ls=["a", "b", "c", "d"])
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_transport_budget for object Modflow6Simulation...'
Arguments: ()
Visualize the last concentration profiles of the model run for the different species.
concentration.isel(time=-1, y=0).plot(x="x", hue="species")
[<matplotlib.lines.Line2D object at 0x000001466D221F90>, <matplotlib.lines.Line2D object at 0x000001466D220CD0>, <matplotlib.lines.Line2D object at 0x000001466D223750>, <matplotlib.lines.Line2D object at 0x000001466D220A50>]
Total running time of the script: (0 minutes 3.841 seconds)