Freshwater Lens

This 2D examples illustrates the growth of a fresh water lens in an initially fully saline domain.

import matplotlib.pyplot as plt

We’ll start with the usual imports

import numpy as np
import xarray as xr

import imod

Discretization

We’ll start off by creating a model discretization, since this is a simple conceptual model. The model is a 2D cross-section, hence nrow = 1.

nrow = 1  # number of rows
ncol = 40  # number of columns
nlay = 15  # number of layers

dz = 10
dx = 250
dy = -dx

Set up tops and bottoms

top1D = xr.DataArray(
    np.arange(nlay * dz, 0.0, -dz), {"layer": np.arange(1, nlay + 1)}, ("layer")
)

bot = top1D - dz

Set up ibound, which sets where active cells are (ibound = 1.0)

bnd = xr.DataArray(
    data=np.full((nlay, nrow, ncol), 1.0),
    coords={
        "y": [0.5],
        "x": np.arange(0.5 * dx, dx * ncol, dx),
        "layer": np.arange(1, 1 + nlay),
        "dx": dx,
        "dy": dy,
    },
    dims=("layer", "y", "x"),
)

Boundary Conditions

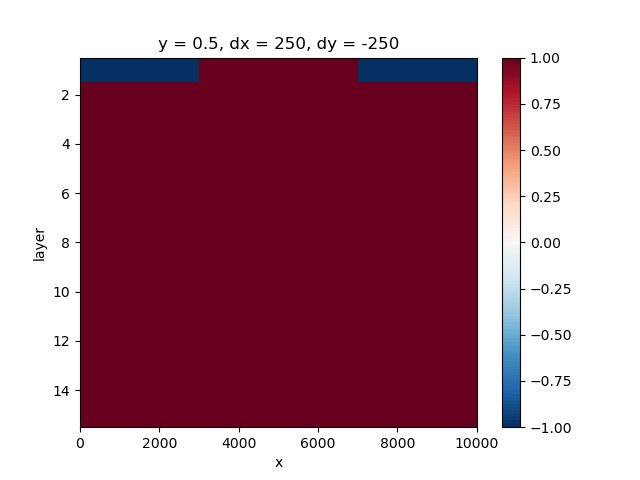
Set the constant heads by specifying a negative value in iboud, that is: bnd[index] = -1`

bnd[0, :, 0:12] = -1
bnd[0, :, 28:40] = -1

fig, ax = plt.subplots()
bnd.plot(y="layer", yincrease=False, ax=ax)

<matplotlib.collections.QuadMesh object at 0x0000017F815940D0>

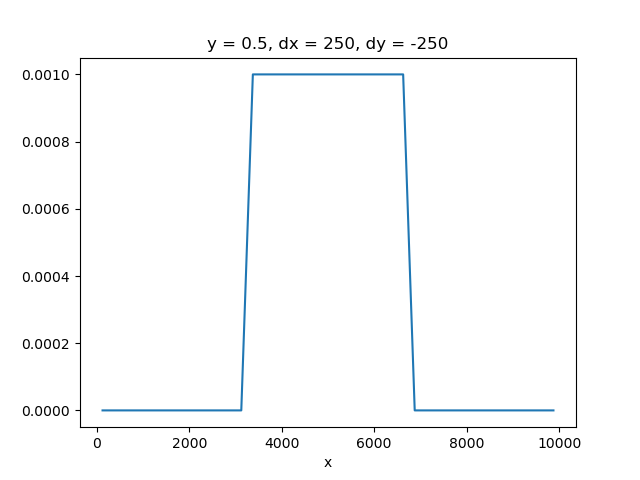
Define the recharge rates

rch_rate = xr.DataArray(
    data=np.full((nrow, ncol), 0.0),
    coords={"y": [0.5], "x": np.arange(0.5 * dx, dx * ncol, dx), "dx": dx, "dy": dy},
    dims=("y", "x"),
)
rch_rate[:, 13:27] = 0.001

fig, ax = plt.subplots()
rch_rate.plot(ax=ax)

[<matplotlib.lines.Line2D object at 0x0000017F8AB828D0>]

The model is recharged with fresh water

rch_conc = xr.full_like(rch_rate, fill_value=0.0)

Initial Conditions

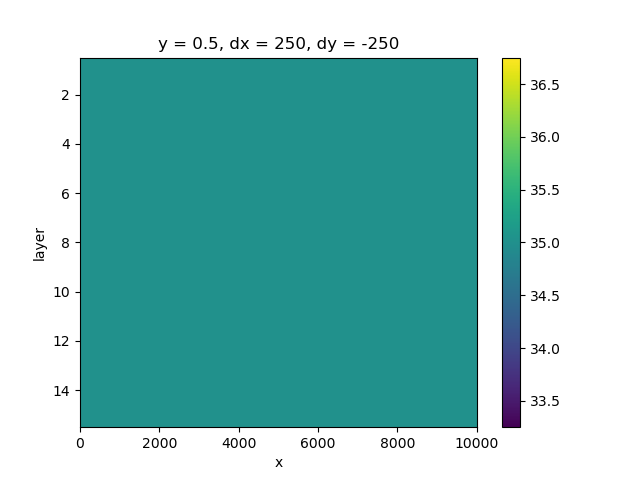
Defining the starting concentrations

sconc = xr.DataArray(
    data=np.full((nlay, nrow, ncol), 35.0),
    coords={
        "y": [0.5],
        "x": np.arange(0.5 * dx, dx * ncol, dx),
        "layer": np.arange(1, nlay + 1),
        "dx": dx,
        "dy": dy,
    },
    dims=("layer", "y", "x"),
)

sconc[:, 13:27, 0] = 0.0

fig, ax = plt.subplots()
sconc.plot(y="layer", yincrease=False, ax=ax)

<matplotlib.collections.QuadMesh object at 0x0000017F8AA70E50>

Build

Finally, we build the model.

m = imod.wq.SeawatModel("FreshwaterLens")
m["bas"] = imod.wq.BasicFlow(ibound=bnd, top=150.0, bottom=bot, starting_head=0.0)
m["lpf"] = imod.wq.LayerPropertyFlow(
    k_horizontal=10.0, k_vertical=20.0, specific_storage=0.0
)
m["btn"] = imod.wq.BasicTransport(
    icbund=bnd, starting_concentration=sconc, porosity=0.35
)
m["adv"] = imod.wq.AdvectionTVD(courant=1.0)
m["dsp"] = imod.wq.Dispersion(longitudinal=0.0, diffusion_coefficient=0.0)
m["vdf"] = imod.wq.VariableDensityFlow(density_concentration_slope=0.71)
m["rch"] = imod.wq.RechargeHighestActive(rate=rch_rate, concentration=0.0)
m["pcg"] = imod.wq.PreconditionedConjugateGradientSolver(
    max_iter=150, inner_iter=30, hclose=0.0001, rclose=0.1, relax=0.98, damp=1.0
)
m["gcg"] = imod.wq.GeneralizedConjugateGradientSolver(
    max_iter=150,
    inner_iter=30,
    cclose=1.0e-6,
    preconditioner="mic",
    lump_dispersion=True,
)
m["oc"] = imod.wq.OutputControl(save_head_idf=True, save_concentration_idf=True)
m.create_time_discretization(additional_times=["1900-01-01T00:00", "2000-01-01T00:00"])

Now we write the model, including runfile:

modeldir = imod.util.temporary_directory()
m.write(modeldir, resultdir_is_workdir=True)

Run

You can run the model using the comand prompt and the iMOD-WQ executable. This is part of the iMOD v5 release, which can be downloaded here: https://oss.deltares.nl/web/imod/download-imod5 . This only works on Windows.

To run your model, open up a command prompt and run the following commands:

cd c:\path\to\modeldir
c:\path\to\imod\folder\iMOD-WQ_V5_3_SVN359_X64R.exe FreshwaterLens.run

Note that the version name of your executable might differ.

Visualise results

After succesfully running the model, you can plot results as follows:

head = imod.idf.open(modeldir / "results/head/*.idf")

fig, ax = plt.subplots()
head.plot(yincrease=False, ax=ax)

conc = imod.idf.open(modeldir / "results/conc/*.idf")

fig, ax = plt.subplots()
conc.plot(levels=range(0, 35, 5), yincrease=False, ax=ax)