Note
Go to the end to download the full example code.
Freshwater lens (circle)#
This example illustrates how to setup a very simple unstructured groundwater
transport model using the imod package and associated packages.
In overview, we’ll set the following steps:
Setting up the flow model, just like in the Circle example
set up the transport model
Run the simulation.
Visualize the results.
We’ll start with the following imports:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import xarray as xr
import xugrid as xu
import imod
Parameters#
porosity = 0.10
max_concentration = 35.0
min_concentration = 0.0
max_density = 1025.0
min_density = 1000.0
k_value = 10.0
Create a mesh#
The first steps consists of generating a mesh. In this example, we’ll use data included with iMOD Python for a circular mesh. Note that this is a Ugrid2D object. For more information on working with unstructured grids see the Xugrid documentation
grid_triangles = imod.data.circle()
fig, ax = plt.subplots()
xu.plot.line(grid_triangles)
ax.set_aspect(1)
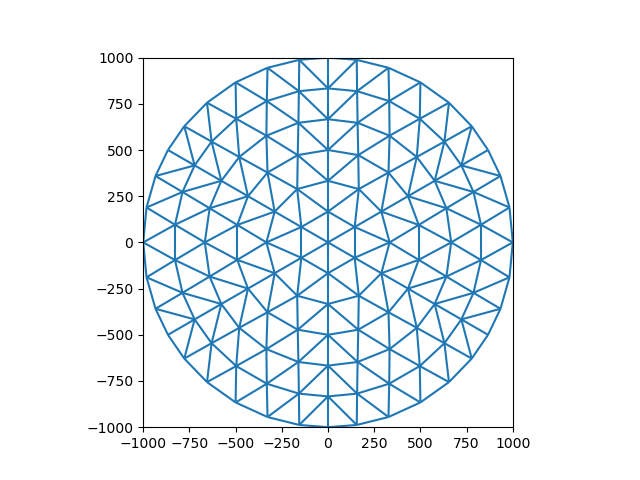
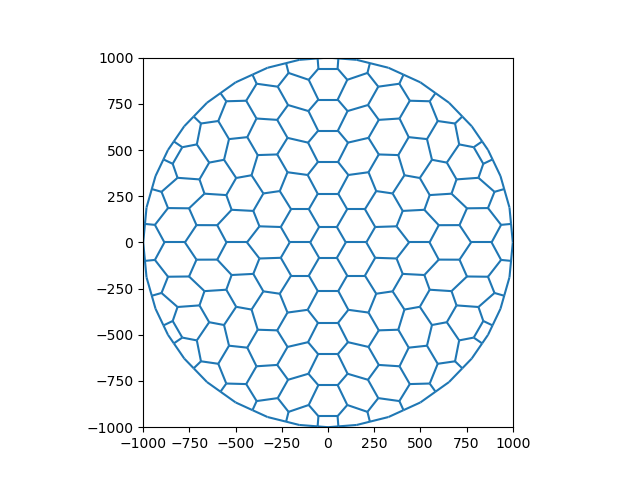
However a triangular grid has the issue that the direction of the fluxes between cell centres is not perpendicular to the cell vertices. The default formulation of MODFLOW 6 does not account for this, which causes mass balance errors. The XT3D formulation is able to account for this, but the last version of MODFLOW 6 (6.3 at time of writing) does not support this in combination with the Buoyancy package and using XT3D comes with an extra, significant computational burden. It is therefore easier to use a voronoi grid, for which Xugrid has a very convenient method.
grid = grid_triangles.tesselate_centroidal_voronoi()
fig, ax = plt.subplots()
xu.plot.line(grid)
ax.set_aspect(1)
Create arrays
nface = grid.n_face
nlayer = 15
layer = np.arange(nlayer, dtype=int) + 1
idomain = xu.UgridDataArray(
xr.DataArray(
np.ones((nlayer, nface), dtype=np.int32),
coords={"layer": layer},
dims=["layer", grid.face_dimension],
),
grid=grid,
)
icelltype = xu.full_like(idomain, 0)
k = xu.full_like(idomain, k_value, dtype=float)
k33 = k.copy()
top = 0.0
bottom = xr.DataArray(top - (layer * 10.0), dims=["layer"])
Recharge#
We need a recharge rate for the fluid and a recharge rate for the solute. The fluid recharge rate is volumetric and per unit area, so the unit is length/time. The solute recharge rate is the concentration of solute in the recharge, and has concentration units.
rch_rate = xu.full_like(idomain.sel(layer=1), 0.001, dtype=float)
rch_concentration = xu.full_like(rch_rate, min_concentration)
rch_concentration = rch_concentration.expand_dims(species=["salinity"])
Unlike a recharge boundary, with a prescribed head boundary we don’t know a priori whether water will flow in over the boundary or leave across the boundary. If water flows into the model over the boundary, it carries a prescribed solute concentration. If it leaves, it leaves with the concentration that was computed for the cell.
In this example we set the prescribed head value to 0.0 and the external concentration to 35.0 as well. The boundary only operates on the top layer.
ghb_location = xu.zeros_like(idomain.sel(layer=1), dtype=bool).ugrid.binary_dilation(
border_value=True
)
constant_head = xu.full_like(idomain, 0.0, dtype=float).where(ghb_location)
conductance = (idomain * grid.area * k_value).where(ghb_location)
constant_concentration = xu.full_like(constant_head, max_concentration).where(
ghb_location
)
constant_concentration = constant_concentration.expand_dims(species=["salinity"])
Add flow model to simulation#
See the Circle example for more information.
gwf_model = imod.mf6.GroundwaterFlowModel()
gwf_model["disv"] = imod.mf6.VerticesDiscretization(
top=top, bottom=bottom, idomain=idomain
)
gwf_model["ghb"] = imod.mf6.GeneralHeadBoundary(
constant_head,
conductance=conductance,
concentration=constant_concentration,
print_input=True,
print_flows=True,
save_flows=True,
)
gwf_model["ic"] = imod.mf6.InitialConditions(start=0.0)
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
icelltype=icelltype,
k=k,
k33=k33,
save_flows=True,
)
gwf_model["sto"] = imod.mf6.SpecificStorage(
specific_storage=1.0e-5,
specific_yield=0.15,
transient=False,
convertible=0,
)
gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")
gwf_model["rch"] = imod.mf6.Recharge(
rch_rate, concentration=rch_concentration, print_flows=True, save_flows=True
)
simulation = imod.mf6.Modflow6Simulation("circle")
simulation["flow"] = gwf_model
simulation["flow_solver"] = imod.mf6.Solution(
modelnames=["flow"],
print_option="summary",
outer_dvclose=1.0e-4,
outer_maximum=500,
under_relaxation=None,
inner_dvclose=1.0e-4,
inner_rclose=0.001,
inner_maximum=100,
linear_acceleration="bicgstab",
scaling_method=None,
reordering_method=None,
relaxation_factor=0.97,
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 139, in <module>
gwf_model = imod.mf6.GroundwaterFlowModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterFlowModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 139, in <module>
gwf_model = imod.mf6.GroundwaterFlowModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 120, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 140, in <module>
gwf_model["disv"] = imod.mf6.VerticesDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the VerticesDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 140, in <module>
gwf_model["disv"] = imod.mf6.VerticesDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 104, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 178, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 143, in <module>
gwf_model["ghb"] = imod.mf6.GeneralHeadBoundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GeneralHeadBoundary package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 143, in <module>
gwf_model["ghb"] = imod.mf6.GeneralHeadBoundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ghb.py", line 170, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ghb.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object GeneralHeadBoundary...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 151, in <module>
gwf_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 151, in <module>
gwf_model["ic"] = imod.mf6.InitialConditions(start=0.0)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 152, in <module>
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the NodePropertyFlow package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 152, in <module>
gwf_model["npf"] = imod.mf6.NodePropertyFlow(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 423, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 158, in <module>
gwf_model["sto"] = imod.mf6.SpecificStorage(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SpecificStorage package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 158, in <module>
gwf_model["sto"] = imod.mf6.SpecificStorage(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\sto.py", line 187, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 164, in <module>
gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 164, in <module>
gwf_model["oc"] = imod.mf6.OutputControl(save_head="last", save_budget="last")
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 165, in <module>
gwf_model["rch"] = imod.mf6.Recharge(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Recharge package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 165, in <module>
gwf_model["rch"] = imod.mf6.Recharge(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 170, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 171, in <module>
simulation["flow_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Solution package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 171, in <module>
simulation["flow_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ims.py", line 451, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Solution...'
Arguments: ()
Time discretization#
Set the timesteps, we want output each year, so we specify stress periods which last 1 year. We add the additional times to ensure that there is output at the end of each year. To achieve this we setup stress periods were each stress period is a year long. We can then use the “last” keyword in the output control to save the output.
simtimes = pd.date_range(start="2000-01-01", end="2030-01-01", freq="YS")
simulation.create_time_discretization(additional_times=simtimes)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 198, in <module>
simulation.create_time_discretization(additional_times=simtimes)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.create_time_discretization for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 198, in <module>
simulation.create_time_discretization(additional_times=simtimes)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
self["time_discretization"] = imod.mf6.TimeDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the TimeDiscretization package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 198, in <module>
simulation.create_time_discretization(additional_times=simtimes)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 249, in create_time_discretization
self["time_discretization"] = imod.mf6.TimeDiscretization(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\timedis.py", line 74, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object TimeDiscretization...'
Arguments: ()
We want to use adaptive time stepping to ensure stable results without taking
an unnecessary amount of small timesteps. We set the initial time step to 0.1
day, the minimum time step to 0.1 day, and the maximum time step to 50 days.
The multiplier is set to 2.0 so that consecutive timesteps will be increased
by a factor of 2 if the convergence is good. Furthermore, we will set the
ats_percel to 0.95 in the Advection package in the next section to let
MODFLOW 6 compute an appropriate time step based on the velocity field: A
solute parcel should not travel more than one cell in a time step. From these
two criteria MODFLOW 6 will select the smallest time step.
simulation["ats"] = imod.mf6.AdaptiveTimeStepping(
dt_init=1e-1,
dt_min=1e-1,
dt_max=50.0,
dt_multiplier=2.0,
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 212, in <module>
simulation["ats"] = imod.mf6.AdaptiveTimeStepping(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ats.py", line 174, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ats.py", line 214, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdaptiveTimeStepping...'
Arguments: ()
Buoyancy#
Since we are solving a variable density problem, we need to add the buoyancy package. It will use the species “salinity” that we are simulating with a transport model defined below.
slope = (max_density - min_density) / (max_concentration - min_concentration)
gwf_model["buoyancy"] = imod.mf6.Buoyancy(
reference_density=min_density,
modelname=["transport"],
reference_concentration=[min_concentration],
density_concentration_slope=[slope],
species=["salinity"],
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 227, in <module>
gwf_model["buoyancy"] = imod.mf6.Buoyancy(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Buoyancy package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 227, in <module>
gwf_model["buoyancy"] = imod.mf6.Buoyancy(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\buy.py", line 113, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Buoyancy...'
Arguments: ()
Add transport model to simulation#
The transport model requires the flow field inside the domain computed by the flow model. It also needs the fluxes over the boundary. It uses the same discretization as the flow model. Here we create a transport model for salinity, derive sources and sinks based from the flow model, and tell it to use the same discretization.
transport_model = imod.mf6.GroundwaterTransportModel()
transport_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
gwf_model, "salinity"
)
transport_model["disv"] = gwf_model["disv"]
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 245, in <module>
transport_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 245, in <module>
transport_model = imod.mf6.GroundwaterTransportModel()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 246, in <module>
transport_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the SourceSinkMixing package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 246, in <module>
transport_model["ssm"] = imod.mf6.SourceSinkMixing.from_flow_model(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 202, in from_flow_model
return SourceSinkMixing(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ssm.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
Now we define some transport packages for simulating the physical processes of advection, mechanical dispersion, and molecular diffusion dispersion. This example is transient, and the volume available for storage is the porosity, in this case 0.10.
al = 0.001
transport_model["dsp"] = imod.mf6.Dispersion(
diffusion_coefficient=1e-4,
longitudinal_horizontal=al,
transversal_horizontal1=al * 0.1,
transversal_vertical=al * 0.01,
xt3d_off=False,
xt3d_rhs=False,
)
transport_model["adv"] = imod.mf6.AdvectionTVD(ats_percel=0.95)
transport_model["mst"] = imod.mf6.MobileStorageTransfer(porosity)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 259, in <module>
transport_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Dispersion package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 259, in <module>
transport_model["dsp"] = imod.mf6.Dispersion(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 181, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 267, in <module>
transport_model["adv"] = imod.mf6.AdvectionTVD(ats_percel=0.95)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\adv.py", line 43, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object AdvectionTVD...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 268, in <module>
transport_model["mst"] = imod.mf6.MobileStorageTransfer(porosity)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the MobileStorageTransfer package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 268, in <module>
transport_model["mst"] = imod.mf6.MobileStorageTransfer(porosity)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\mst.py", line 134, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
Define the maximum concentration as the initial conditions, also output options for the transport model, and assign the transport model to the simulation as well.
transport_model["ic"] = imod.mf6.InitialConditions(start=max_concentration)
transport_model["oc"] = imod.mf6.OutputControl(
save_concentration="last", save_budget="last"
)
simulation["transport"] = transport_model
simulation["transport_solver"] = imod.mf6.Solution(
modelnames=["transport"],
print_option="summary",
outer_dvclose=1.0e-4,
outer_maximum=500,
under_relaxation=None,
inner_dvclose=1.0e-4,
inner_rclose=0.001,
inner_maximum=100,
linear_acceleration="bicgstab",
scaling_method=None,
reordering_method=None,
relaxation_factor=0.97,
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 275, in <module>
transport_model["ic"] = imod.mf6.InitialConditions(start=max_concentration)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the InitialConditions package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 275, in <module>
transport_model["ic"] = imod.mf6.InitialConditions(start=max_concentration)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ic.py", line 75, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 276, in <module>
transport_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the OutputControl package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 276, in <module>
transport_model["oc"] = imod.mf6.OutputControl(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 114, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 281, in <module>
simulation["transport_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the Solution package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 281, in <module>
simulation["transport_solver"] = imod.mf6.Solution(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ims.py", line 451, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Solution...'
Arguments: ()
We’ll create a new directory in which we will write and run the model.
modeldir = imod.util.temporary_directory() / "full"
simulation.write(modeldir, binary=False)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.write for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 178, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ghb.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object GeneralHeadBoundary...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Buoyancy...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GeneralHeadBoundary...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Buoyancy...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 178, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionTVD...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 300, in <module>
simulation.write(modeldir, binary=False)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
Run the model#
Note
The following lines assume the mf6 executable is available on your
PATH. The examples introduction shortly describes how to add it to yours.
simulation.run()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 311, in <module>
simulation.run()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.run for object Modflow6Simulation...'
Arguments: ()
Open the results#
sim_concentration = simulation.open_concentration().compute().reindex_like(idomain)
sim_head = simulation.open_head().compute().reindex_like(idomain)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 317, in <module>
sim_concentration = simulation.open_concentration().compute().reindex_like(idomain)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_concentration for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 318, in <module>
sim_head = simulation.open_head().compute().reindex_like(idomain)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_head for object Modflow6Simulation...'
Arguments: ()
Assign coordinates to output#
The model output does not feature very useful coordinate values for time
and z, therefore it is best to assign these to the datasets for more
understandable plots.
First we have to compute values for a z coordinate. The
interfaces = np.concatenate([[top], bottom.values])
z = (interfaces[:-1] + interfaces[1:]) / 2
z
array([ -5., -15., -25., -35., -45., -55., -65., -75., -85.,
-95., -105., -115., -125., -135., -145.])
Assign these new coordinate values to the dataset
coords = {"time": simtimes[1:], "z": ("layer", z)}
sim_head = sim_head.assign_coords(**coords)
sim_concentration = sim_concentration.assign_coords(**coords)
Visualize the results#
We can quickly and easily visualize the output with the plotting functions provided by xarray and xugrid:
fig, ax = plt.subplots()
sim_head.isel(time=-1, layer=0).ugrid.plot(ax=ax)
ax.set_aspect(1)
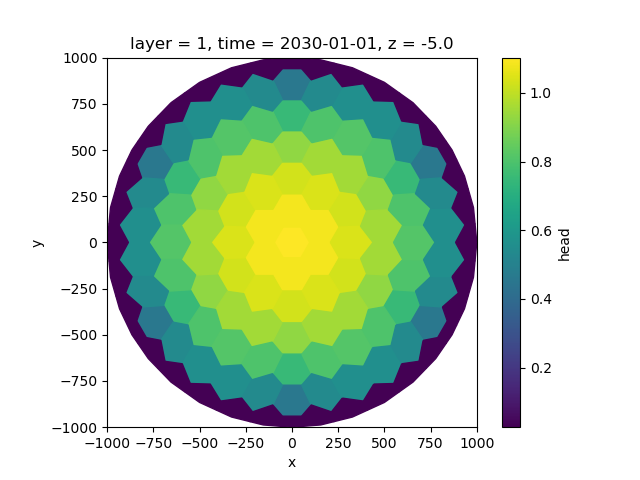
We can draw a crossection through the center by selecting y=0, for which we can plot the contours as follows:
fig, ax = plt.subplots()
sim_concentration.isel(time=-1).ugrid.sel(y=0).plot.contourf(
ax=ax, x="mesh2d_x", y="z", cmap="RdYlBu_r"
)
<matplotlib.contour.QuadContourSet object at 0x00000146680187D0>
Slice the model domain#
We may also quickly setup a smaller model. We’ll select half of the original domain. To set up the boundary conditions on the clipped edges you can provide a states_for_boundary dictionary. In this case we add the head values for the flow model and the concentration values for the transport model of the computed full domain simulation as the clipped boundary values. You can use this feature to clip a smaller model from an existing larger model, downscale it, and conduct a study in more detail around an area of interest.
states_for_boundary = {
"flow": sim_head.isel(time=-1, drop=True).drop_vars("z"),
"transport": sim_concentration.isel(time=-1, drop=True).drop_vars("z"),
}
half_simulation = simulation.clip_box(
x_max=0.1, states_for_boundary=states_for_boundary
)
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.clip_box for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 804, in clip_box
clipped = self._clip_box_packages(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 861, in _clip_box_packages
clipped = type(self)(**self._options)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterFlowModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 804, in clip_box
clipped = self._clip_box_packages(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 861, in _clip_box_packages
clipped = type(self)(**self._options)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 120, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 100, in _create_boundary_condition_clipped_boundary
_create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantHead package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 100, in _create_boundary_condition_clipped_boundary
_create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 152, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 124, in _create_boundary_condition_clipped_boundary
bc_constant_pkg = _create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantHead package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 124, in _create_boundary_condition_clipped_boundary
bc_constant_pkg = _create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 152, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 816, in clip_box
clipped.purge_empty_packages(ignore_time=ignore_time_purge_empty)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 957, in purge_empty_packages
logger.info(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'packages: [] removed in , because all empty'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 804, in clip_box
clipped = self._clip_box_packages(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 861, in _clip_box_packages
clipped = type(self)(**self._options)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GroundwaterTransportModel package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 804, in clip_box
clipped = self._clip_box_packages(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 861, in _clip_box_packages
clipped = type(self)(**self._options)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwt.py", line 65, in __init__
self._validate_init_schemata_options(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 179, in _validate_init_schemata_options
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 100, in _create_boundary_condition_clipped_boundary
_create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantConcentration package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 100, in _create_boundary_condition_clipped_boundary
_create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\cnc.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantConcentration...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 124, in _create_boundary_condition_clipped_boundary
bc_constant_pkg = _create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the ConstantConcentration package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 808, in clip_box
clipped_boundary_condition = _create_boundary_condition_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 124, in _create_boundary_condition_clipped_boundary
bc_constant_pkg = _create_boundary_condition_for_unassigned_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 84, in _create_boundary_condition_for_unassigned_boundary
return create_clipped_boundary(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\utilities\clipped_bc_creator.py", line 154, in create_clipped_boundary
return pkg_type(constant_state, print_input=True, print_flows=True, save_flows=True)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 64, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\cnc.py", line 88, in __init__
self._validate_init_schemata(validate)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\package.py", line 365, in _validate_init_schemata
validate_with_error_message(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\common\utilities\schemata.py", line 132, in validate_with_error_message
errors = validate_func(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantConcentration...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 378, in <module>
half_simulation = simulation.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1303, in clip_box
clipped[key] = value.clip_box(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 816, in clip_box
clipped.purge_empty_packages(ignore_time=ignore_time_purge_empty)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 957, in purge_empty_packages
logger.info(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'packages: [] removed in , because all empty'
Arguments: ()
Let’s run the model, read the results, and visualize.
modeldir = imod.util.temporary_directory() / "half"
half_simulation.write(modeldir)
half_simulation.run()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.write for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 353, in write
if gwfgwt_exchanges := self._generate_gwfgwt_exchanges():
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 1683, in _generate_gwfgwt_exchanges
exchanges.append(GWFGWT(flow_name, transport_model_name))
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 61, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Initializing the GWFGWT package...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterFlowModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 178, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\ghb.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object GeneralHeadBoundary...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\npf.py", line 455, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\rch.py", line 175, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Buoyancy...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model_gwf.py", line 192, in validate
return super().validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\chd.py", line 157, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GeneralHeadBoundary...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object NodePropertyFlow...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SpecificStorage...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Recharge...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Buoyancy...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object ConstantHead...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._write for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model.validate for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 398, in validate
option_errors = self._validate_options(self._init_schemata)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.model._validate_options for object GroundwaterTransportModel...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\disv.py", line 178, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\dsp.py", line 186, in _validate
errors = super()._validate(schemata, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 546, in _write
model_status_info = self.validate(modelname, validate_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 415, in validate
pkg_errors = pkg._validate(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._validate for object ConstantConcentration...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object SourceSinkMixing...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object VerticesDiscretization...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Dispersion...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object AdvectionTVD...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object MobileStorageTransfer...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object InitialConditions...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\oc.py", line 194, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object OutputControl...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 380, in write
value._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\model.py", line 574, in _write
pkg._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\boundary_condition.py", line 297, in _write
super()._write(pkgname, globaltimes, write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object ConstantConcentration...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 395, in write
value._write(key, globaltimes, pkg_write_context)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object Solution...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 966, in _exec_and_get_memory
mem_body, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 386, in <module>
half_simulation.write(modeldir)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 32, in wrapper
return_value = fun(*args, **kwargs)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\mf6\simulation.py", line 399, in write
exchange._write(
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.package._write for object GWFGWT...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 976, in _exec_and_get_memory
mem_last, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 387, in <module>
half_simulation.run()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.run for object Modflow6Simulation...'
Arguments: ()
Open the results#
half_sim_concentration = half_simulation.open_concentration().compute()
half_sim_head = half_simulation.open_head().compute()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 393, in <module>
half_sim_concentration = half_simulation.open_concentration().compute()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_concentration for object Modflow6Simulation...'
Arguments: ()
--- Logging error ---
Traceback (most recent call last):
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\logging\__init__.py", line 1154, in emit
stream.write(msg + self.terminator)
~~~~~~~~~~~~^^^^^^^^^^^^^^^^^^^^^^^
ValueError: I/O operation on closed file.
Call stack:
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Scripts\sphinx-build-script.py", line 10, in <module>
sys.exit(main())
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 491, in main
return make_mode.run_make_mode(argv[1:])
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 223, in run_make_mode
return make.run_generic_build(builder_name)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\make_mode.py", line 206, in run_generic_build
return build_main(args + self.opts)
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\cmd\build.py", line 414, in build_main
app = Sphinx(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 340, in __init__
self._init_builder()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\application.py", line 430, in _init_builder
self.events.emit('builder-inited')
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx\events.py", line 441, in emit
results.append(listener.handler(self._app, *args))
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_gallery.py", line 788, in generate_gallery_rst
) = generate_dir_rst(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 679, in generate_dir_rst
results = parallel(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 680, in <genexpr>
p_fun(fname, target_dir, src_dir, gallery_conf) for fname in iterator
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1520, in generate_file_rst
output_blocks, time_elapsed = execute_script(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1321, in execute_script
execute_code_block(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1170, in execute_code_block
is_last_expr, mem_max = _exec_and_get_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 984, in _exec_and_get_memory
mem_max, _ = call_memory(
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 1895, in _sg_call_memory_noop
return 0.0, func()
File "C:\pixi_envs\imod-python-1825887385235446013\envs\default\Lib\site-packages\sphinx_gallery\gen_rst.py", line 891, in __call__
exec(self.code, self.fake_main.__dict__)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\examples\mf6\circle_transport.py", line 394, in <module>
half_sim_head = half_simulation.open_head().compute()
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\logging_decorators.py", line 29, in wrapper
logger.log(loglevel=start_level, message=start_message, additional_depth=2)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\ilogger.py", line 94, in log
self.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\_loggerholder.py", line 56, in info
self.instance.info(message, additional_depth)
File "C:\buildagent\work\4b9080cbb3354582\imod-python\imod\logging\pythonlogger.py", line 52, in info
self.logger.info(message, stacklevel=_stack_level(additional_depth))
Message: 'Beginning execution of imod.mf6.simulation.open_head for object Modflow6Simulation...'
Arguments: ()
Assign these new coordinate values to the dataset
half_sim_head = half_sim_head.assign_coords(**coords)
half_sim_concentration = half_sim_concentration.assign_coords(**coords)
Visualize the results#
We can quickly and easily visualize the output with the plotting functions provided by xarray and xugrid:
fig, ax = plt.subplots()
half_sim_head.isel(time=-1, layer=0).ugrid.plot(ax=ax)
ax.set_aspect(1)
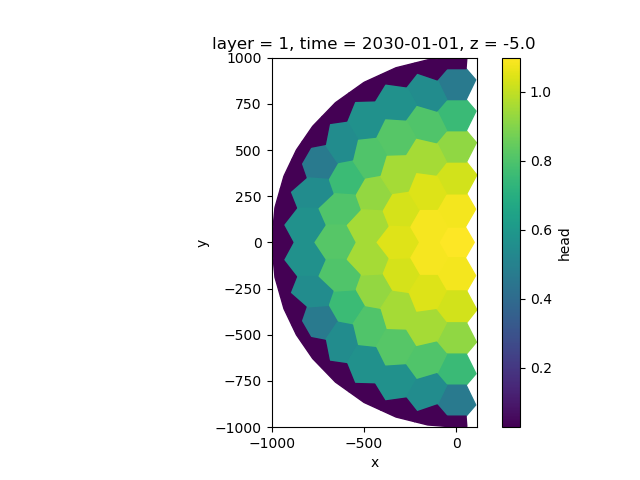
We can draw a crossection through the center by selecting y=0, for which we can plot the contours as follows:
fig, ax = plt.subplots()
half_sim_concentration.isel(time=-1).ugrid.sel(y=0).plot.contourf(
ax=ax, x="mesh2d_x", y="z", cmap="RdYlBu_r"
)
<matplotlib.contour.QuadContourSet object at 0x000001466926A710>
Total running time of the script: (1 minutes 13.875 seconds)