Distribution functions#

In this example, we will demonstrate how to define a distribution function using the probabilistic library.

The library supports the following distribution functions: deterministic, normal, log_normal, uniform, triangular, trapezoidal, exponential, gumbel, weibull, conditional_weibull, frechet, generalized_extreme_value, rayleigh, rayleigh_n, pareto, generalized_pareto, student_t, gamma, beta, poisson, discrete, bernoulli, cdf_curve, histogram. Distribution functions are defined in the distribution property of a stochast.

Define a stochastic variable#

First, we import the necessary classes:

[53]:

from probabilistic_library import Stochast, DistributionType, DiscreteValue, HistogramValue, FragilityValue

Next, we create a random variable:

[54]:

stochast = Stochast()

Below, we demonstrate how to define distribution functions in the library.

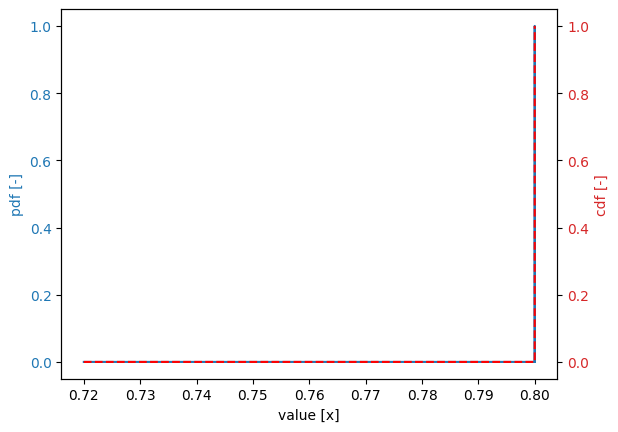
Deterministic distribution#

[55]:

stochast.distribution = DistributionType.deterministic
stochast.mean = 0.8

stochast.print()
stochast.plot()

Variable:
  distribution = deterministic
Definition:
  location = 0.8
Derived values:
  mean = 0.8
  deviation = 0.0
  variation = 0.0
../_images/_examples_overview_distribution_functions_6_1.png

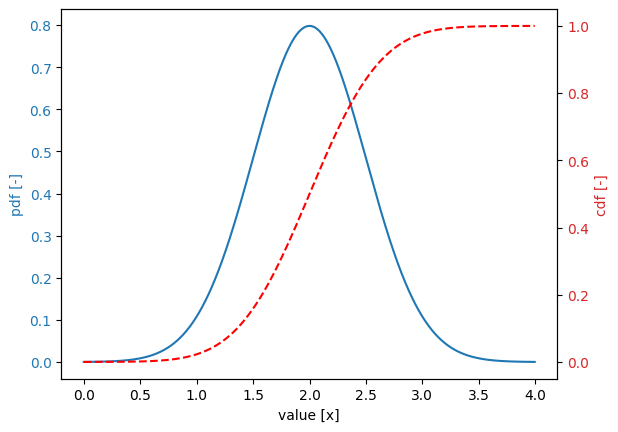
Normal distribution#

[56]:

stochast = Stochast()
stochast.distribution = DistributionType.normal
stochast.location = 2.0
stochast.scale = 0.5

stochast.print()
stochast.plot()

Variable:
  distribution = normal
Definition:
  location = 2.0
  scale = 0.5
Derived values:
  mean = 2.0
  deviation = 0.5
  variation = 0.25
../_images/_examples_overview_distribution_functions_8_1.png

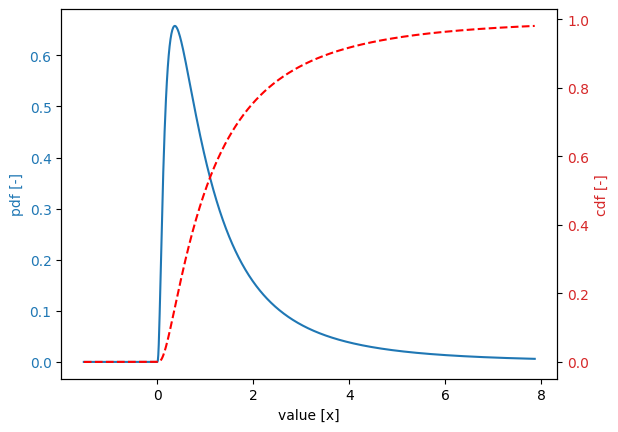
Log-normal distribution#

[57]:

stochast = Stochast()
stochast.distribution = DistributionType.log_normal
stochast.location = 0.0
stochast.scale = 1.0
stochast.shift = 0.0

stochast.print()
stochast.plot()

Variable:
  distribution = log_normal
Definition:
  location = 0.0
  scale = 1.0
  shift = 0.0
Derived values:
  mean = 1.6487
  deviation = 2.1612
  variation = 1.3108
../_images/_examples_overview_distribution_functions_10_1.png

Uniform distribution#

[58]:

stochast = Stochast()
stochast.distribution = DistributionType.uniform
stochast.minimum = -1
stochast.maximum = 1

stochast.print()
stochast.plot()

Variable:
  distribution = uniform
Definition:
  minimum = -1.0
  maximum = 1.0
Derived values:
  mean = 0.0
  deviation = 0.5774
  variation = 0.0
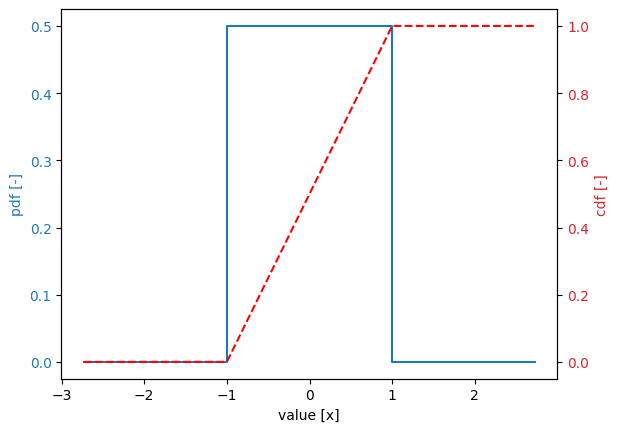
../_images/_examples_overview_distribution_functions_12_1.png

Triangular distribution#

[59]:

stochast = Stochast()
stochast.distribution = DistributionType.triangular
stochast.minimum = 0.0 # parameter a
stochast.maximum = 3.0 # parameter b
stochast.shift = 2.0 # parameter c

stochast.print()
stochast.plot()

Variable:
  distribution = triangular
Definition:
  minimum = 0.0
  shift = 2.0
  maximum = 3.0
Derived values:
  mean = 1.6667
  deviation = 0.6236
  variation = 0.3742
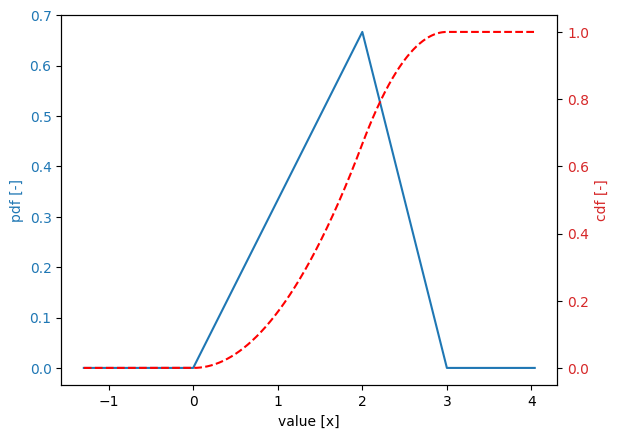
../_images/_examples_overview_distribution_functions_14_1.png

Trapezoidal distribution#

[60]:

stochast = Stochast()
stochast.distribution = DistributionType.trapezoidal
stochast.minimum = 1.0 # parameter a
stochast.maximum = 4.5 # parameter b
stochast.shift = 2.0 # parameter c
stochast.shift_b = 3.0 # parameter d

stochast.print()
stochast.plot()

Variable:
  distribution = trapezoidal
Definition:
  minimum = 1.0
  shift = 2.0
  shift_b = 3.0
  maximum = 4.5
Derived values:
  mean = 2.6481
  deviation = 0.7462
  variation = 0.2818
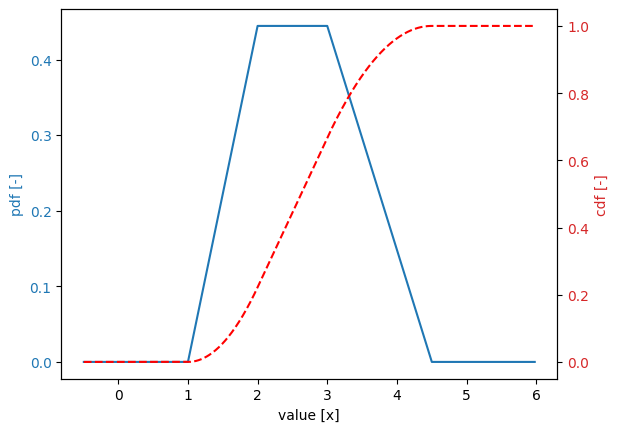
../_images/_examples_overview_distribution_functions_16_1.png

Exponential distribution#

[61]:

stochast = Stochast()
stochast.distribution = DistributionType.exponential
stochast.scale = 2.0
stochast.shift = 0.5

stochast.print()
stochast.plot()

Variable:
  distribution = exponential
Definition:
  scale = 2.0
  shift = 0.5
Derived values:
  mean = 2.5
  deviation = 2.0
  variation = 0.8
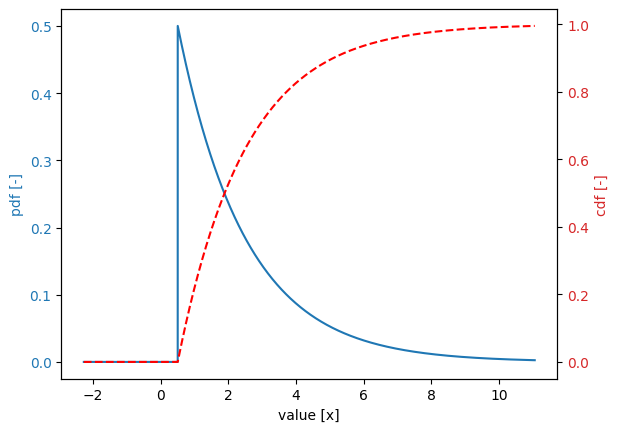
../_images/_examples_overview_distribution_functions_18_1.png

Gumbel distribution#

[62]:

stochast = Stochast()
stochast.distribution = DistributionType.gumbel
stochast.scale = 2.0
stochast.shift = 3.0

stochast.print()
stochast.plot()

Variable:
  distribution = gumbel
Definition:
  scale = 2.0
  shift = 3.0
Derived values:
  mean = 4.1544
  deviation = 2.5651
  variation = 0.6174
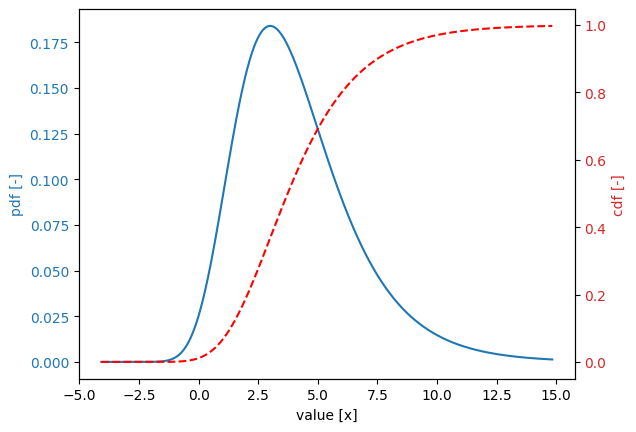
../_images/_examples_overview_distribution_functions_20_1.png

Weibull distribution#

[63]:

stochast = Stochast()
stochast.distribution = DistributionType.weibull
stochast.scale = 1.0
stochast.shift = 1.0
stochast.shape = 2.0

stochast.print()
stochast.plot()

Variable:
  distribution = weibull
Definition:
  scale = 1.0
  shift = 1.0
  shape = 2.0
Derived values:
  mean = 1.8862
  deviation = 0.4633
  variation = 0.2456
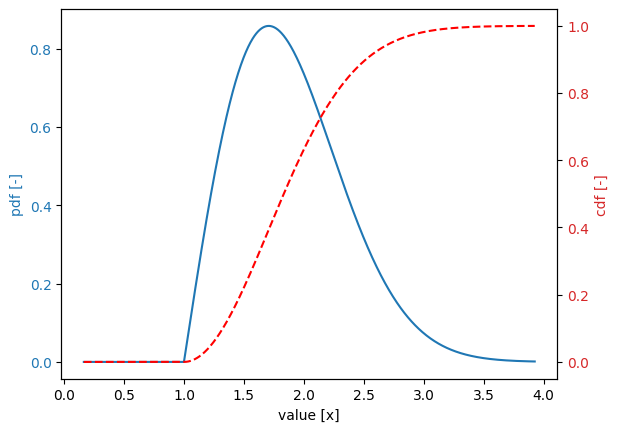
../_images/_examples_overview_distribution_functions_22_1.png

Conditional Weibull distribution#

[64]:

stochast = Stochast()
stochast.distribution = DistributionType.conditional_weibull
stochast.scale = 1.0
stochast.shift = 5.0
stochast.shape = 2.0
stochast.shape_b = 1.0

stochast.print()
stochast.plot()

Variable:
  distribution = conditional_weibull
Definition:
  scale = 1.0
  shift = 5.0
  shape = 2.0
  shape_b = 1.0
Derived values:
  mean = 5.0558
  deviation = 0.1251
  variation = 0.0247
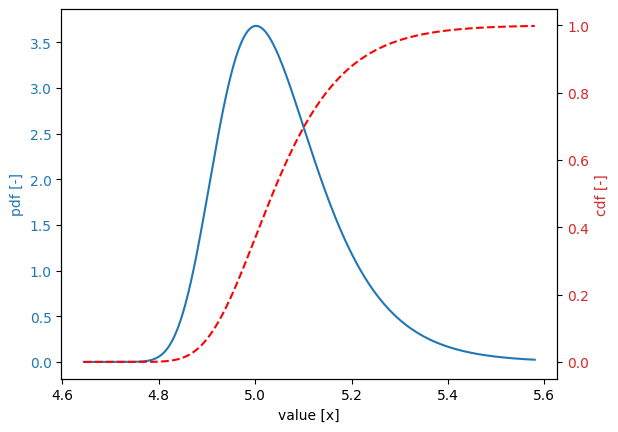
../_images/_examples_overview_distribution_functions_24_1.png

Frechet distribution#

[65]:

stochast = Stochast()
stochast.distribution = DistributionType.frechet
stochast.scale = 0.5
stochast.shift = 1.0
stochast.shape = 2.0

stochast.print()
stochast.plot()

Variable:
  distribution = frechet
Definition:
  scale = 0.5
  shift = 1.0
  shape = 2.0
Derived values:
  mean = 1.8862
  deviation = inf
  variation = inf
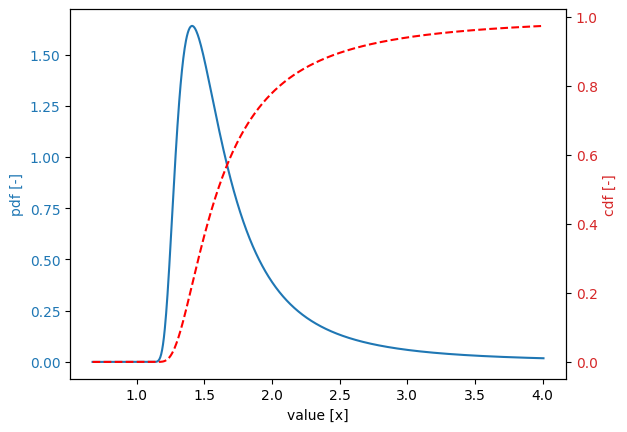
../_images/_examples_overview_distribution_functions_26_1.png

Generalized extreme value distribution#

[66]:

stochast = Stochast()
stochast.distribution = DistributionType.generalized_extreme_value
stochast.scale = 1.0
stochast.shift = 5.0
stochast.shape = -0.5

stochast.print()
stochast.plot()

Variable:
  distribution = generalized_extreme_value
Definition:
  scale = 1.0
  shift = 5.0
  shape = -0.5
Derived values:
  mean = 5.2275
  deviation = 0.9265
  variation = 0.1772
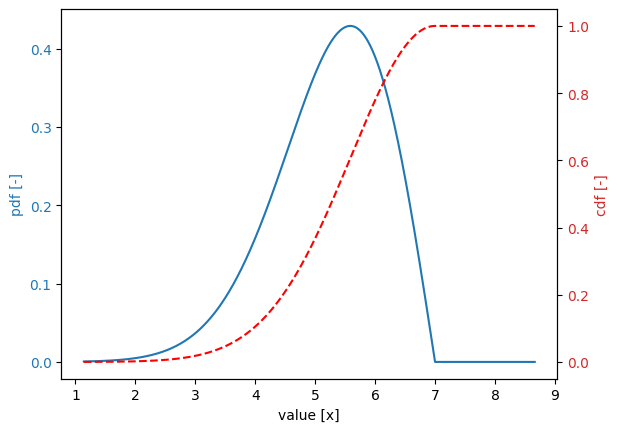
../_images/_examples_overview_distribution_functions_28_1.png

Rayleigh distribution#

[67]:

stochast = Stochast()
stochast.distribution = DistributionType.rayleigh
stochast.scale = 0.5
stochast.shift = 1.0

stochast.print()
stochast.plot()

Variable:
  distribution = rayleigh
Definition:
  scale = 0.5
  shift = 1.0
Derived values:
  mean = 1.6267
  deviation = 0.3276
  variation = 0.2014
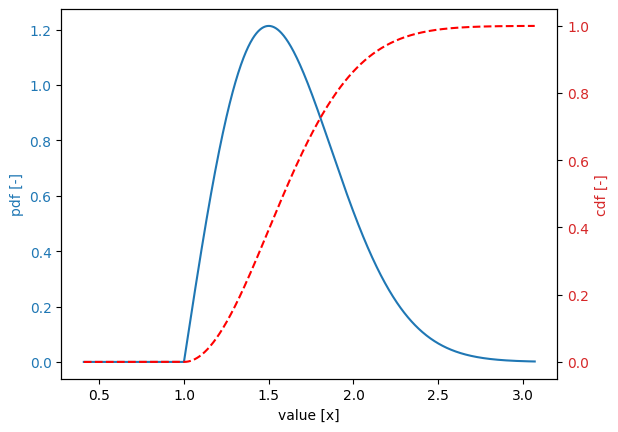
../_images/_examples_overview_distribution_functions_30_1.png

Rayleigh N distribution#

[68]:

stochast = Stochast()
stochast.distribution = DistributionType.rayleigh_n
stochast.scale = 1.0
stochast.shift = 0.0
stochast.shape = 50.0

stochast.print()
stochast.plot()

Variable:
  distribution = rayleigh_n
Definition:
  scale = 1.0
  shift = 0.0
  shape = 50.0
Derived values:
  mean = 2.9718
  deviation = 0.4078
  variation = 0.1372
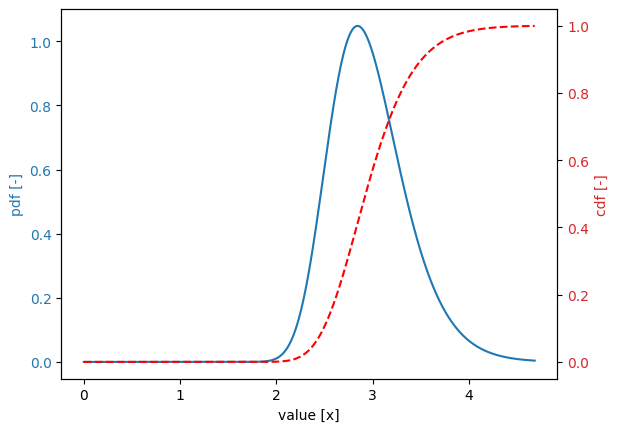
../_images/_examples_overview_distribution_functions_32_1.png

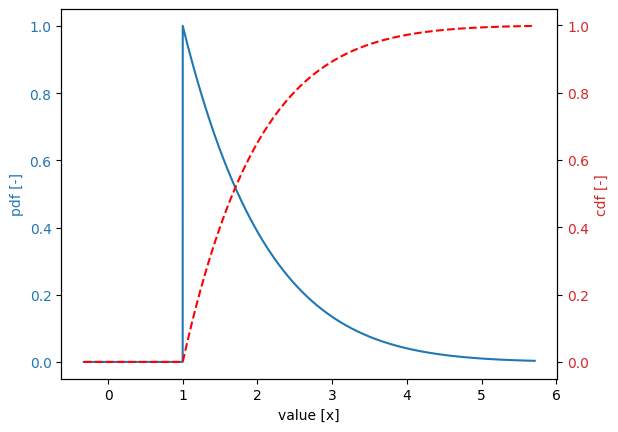
Pareto distribution#

[69]:

stochast = Stochast()
stochast.distribution = DistributionType.pareto
stochast.scale = 1.0
stochast.shape = 3.0

stochast.print()
stochast.plot()

Variable:
  distribution = pareto
Definition:
  scale = 1.0
  shape = 3.0
Derived values:
  mean = 1.5
  deviation = 0.866
  variation = 0.5774
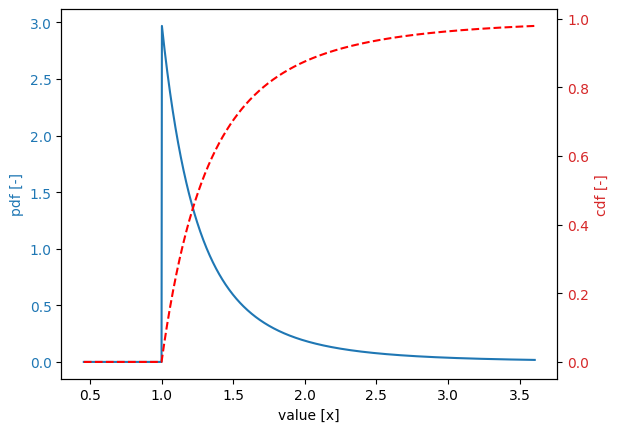
../_images/_examples_overview_distribution_functions_34_1.png

Generalized Pareto distribution#

[70]:

stochast = Stochast()
stochast.distribution = DistributionType.generalized_pareto
stochast.shape = 0.1
stochast.scale = 1.0
stochast.shift = 1.0

stochast.print()
stochast.plot()

Variable:
  distribution = generalized_pareto
Definition:
  scale = 1.0
  shift = 1.0
  shape = 0.1
Derived values:
  mean = 1.909
  deviation = 0.8294
  variation = 0.4345
../_images/_examples_overview_distribution_functions_36_1.png

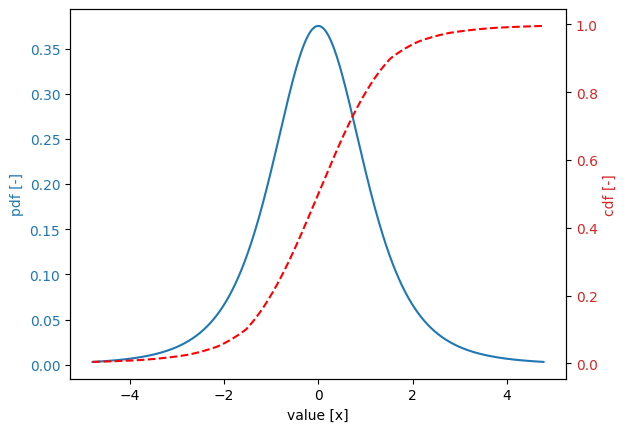
Student’s t-distribution#

[71]:

stochast = Stochast()
stochast.distribution = DistributionType.student_t
stochast.location = 0.0
stochast.scale = 1.0
stochast.observations = 5

stochast.print()
stochast.plot()

Variable:
  distribution = student_t
Definition:
  location = 0.0
  scale = 1.0
  observations = 5
Derived values:
  mean = 0.0
  deviation = 1.4142
  variation = 0.0
../_images/_examples_overview_distribution_functions_38_1.png

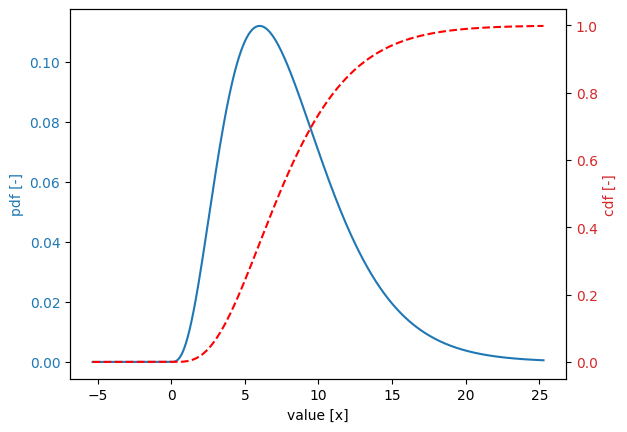
Gamma distribution#

[72]:

stochast = Stochast()
stochast.distribution = DistributionType.gamma
stochast.scale = 2.0
stochast.shape = 4.0

stochast.print()
stochast.plot()

Variable:
  distribution = gamma
Definition:
  scale = 2.0
  shape = 4.0
Derived values:
  mean = 8.0
  deviation = 4.0
  variation = 0.5
../_images/_examples_overview_distribution_functions_40_1.png

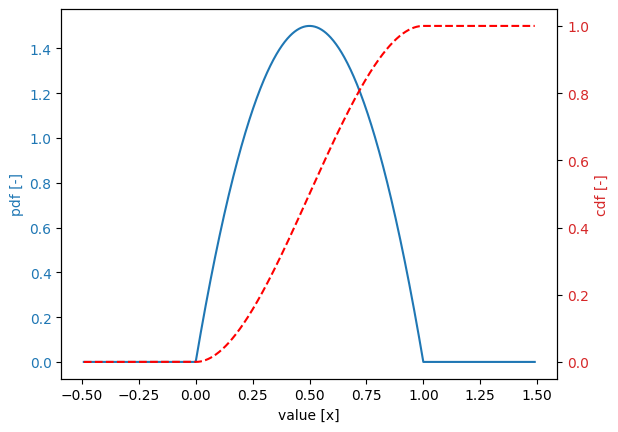
Beta distribution#

[73]:

stochast = Stochast()
stochast.distribution = DistributionType.beta
stochast.shape = 2.0
stochast.shape_b = 2.0

stochast.print()
stochast.plot()

Variable:
  distribution = beta
Definition:
  shape = 2.0
  shape_b = 2.0
Derived values:
  mean = 0.5
  deviation = 0.2236
  variation = 0.4472
../_images/_examples_overview_distribution_functions_42_1.png

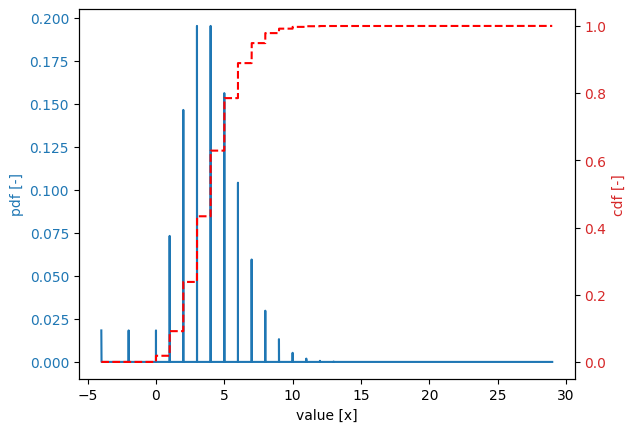
Poisson distribution#

[74]:

stochast = Stochast()
stochast.distribution = DistributionType.poisson
stochast.location = 4.0

stochast.print()
stochast.plot()

Variable:
  distribution = poisson
Definition:
  scale = 0.0
  shift = 0.0
Derived values:
  mean = 4.0
  deviation = 2.0
  variation = 0.5
../_images/_examples_overview_distribution_functions_44_1.png

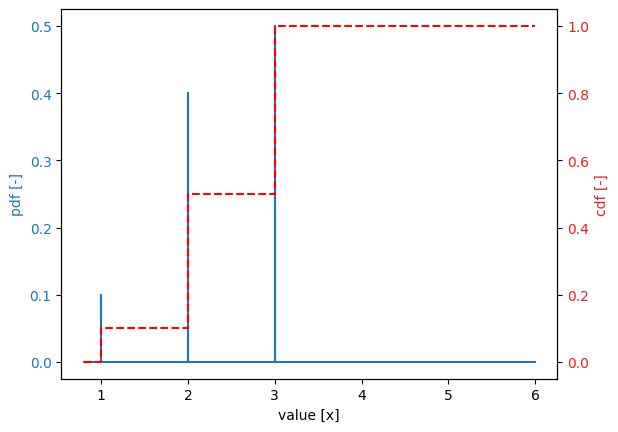
Discrete distribution#

[75]:

stochast = Stochast()
stochast.distribution = DistributionType.discrete

x = [1, 2, 3]
amount = [0.1, 0.4, 0.5]

for i in range(0, len(x)):

    dv = DiscreteValue()
    dv.x = x[i]
    dv.amount = amount[i]

    stochast.discrete_values.append(dv)

stochast.print()
stochast.plot()

Variable:
  distribution = discrete
Definition:
  amount[1.0] = 0.1
  amount[2.0] = 0.4
  amount[3.0] = 0.5
Derived values:
  mean = 2.4
  deviation = 0.6633
  variation = 0.2764
../_images/_examples_overview_distribution_functions_46_1.png

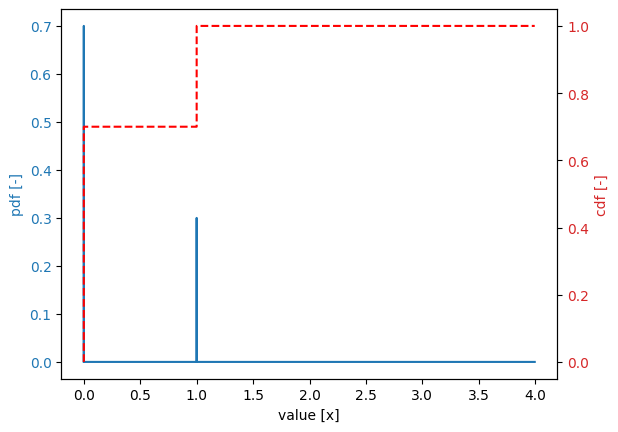
Bernoulli distribution#

[76]:

stochast = Stochast()
stochast.distribution = DistributionType.bernoulli
stochast.location = 0.3

stochast.print()
stochast.plot()

Variable:
  distribution = bernoulli
Definition:
  location = 0.3
Derived values:
  mean = 0.3
  deviation = 0.4583
  variation = 1.5275
../_images/_examples_overview_distribution_functions_48_1.png

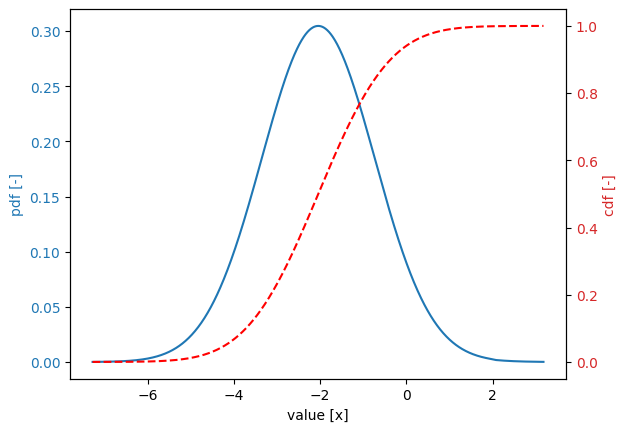
CDF curve distribution#

[77]:

stochast = Stochast()
stochast.distribution =  DistributionType.cdf_curve

x = [1, 2, 3]
probability_of_failure = [0.01, 0.001, 0.0001]
# these are the exceedance probabilities, which will shift the probability mass to an area < 1.0

for i in range(0, len(x)):

    fc = FragilityValue()
    fc.x = x[i]
    fc.probability_of_failure = probability_of_failure[i]

    stochast.fragility_values.append(fc)

stochast.print()
stochast.plot()

Variable:
  distribution = cdf_curve
Definition:
  beta[1.0] = 2.3263
  beta[2.0] = 3.0902
  beta[3.0] = 3.719
Derived values:
  mean = -2.0454
  deviation = 1.3091
  variation = 0.64
../_images/_examples_overview_distribution_functions_50_1.png

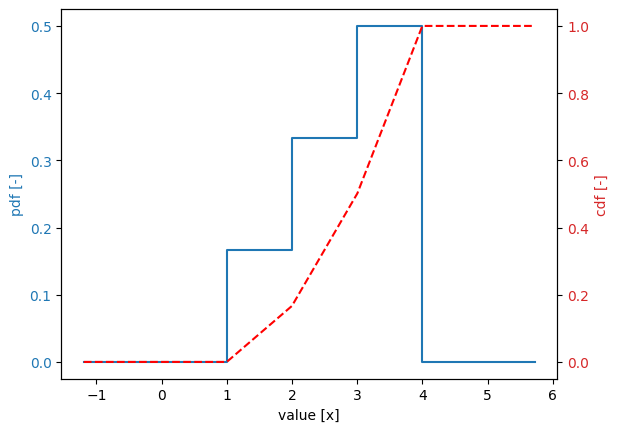
Histogram distribution#

[78]:

stochast = Stochast()
stochast.distribution =  DistributionType.histogram

lower_bound = [1, 2, 3]
upper_bound = [2, 3, 4]
amount = [100, 200, 300]

for i in range(0, len(lower_bound)):

    hv = HistogramValue()
    hv.lower_bound = lower_bound[i]
    hv.upper_bound = upper_bound[i]
    hv.amount = amount[i]
    stochast.histogram_values.append(hv)

stochast.print()
stochast.plot()

Variable:
  distribution = histogram
Definition:
  amount[1.0, 2.0] = 100.0
  amount[2.0, 3.0] = 200.0
  amount[3.0, 4.0] = 300.0
Derived values:
  mean = 2.8333
  deviation = 0.746
  variation = 0.2633
../_images/_examples_overview_distribution_functions_52_1.png
On this page
Edit on GitHub
Show Source