Model with arrays as input#
Reliability calculations with arrays as arguments in the model#
This example demonstrates how to perform reliability calculations with a limit state function that has multiple arguments, all following a similar distribution function.
Define model#
First, let’s import the necessary classes:
[1]:
from probabilistic_library import ReliabilityProject, DistributionType, ReliabilityMethod, Stochast
We consider the following limit state function:
\(Z = 1.9 - [\sum_{i=1}^{n}(a_i)+\sum_{j=1}^{m}(b_j)]\)
This is a linear model involving two arrays, \(a\) and \(b\).
[2]:
from utils.models import linear_arrays
To perform a reliability analysis, we create a reliability project and specify the limit state function (model):
[3]:
project = ReliabilityProject()
project.model = linear_arrays
project.model.print()
Model linear_arrays:
Input parameters:
const_val
a[1]
b[1]
Output parameters:
Z
In this example, we assume that array \(a\) consists of \(25\) variables following a uniform distribution over the interval \([-1, 1]\). Array \(b\) consists of \(30\) variables, each normally distributed with a mean of \(0\) and a standard deviation of \(1\). This can be defined as follows:
[4]:
project.variables["const_val"].distribution = DistributionType.deterministic
project.variables["const_val"].is_array = False
project.variables["const_val"].mean = 1.9
project.variables["a"].distribution = DistributionType.uniform
project.variables["a"].is_array = True # states that a is an array
project.variables["a"].array_size = 25
project.variables["a"].minimum = -1
project.variables["a"].maximum = 1
project.variables["b"].distribution = DistributionType.normal
project.variables["b"].is_array = True # states that b is an array
project.variables["b"].array_size = 30
project.variables["b"].mean = 0
project.variables["b"].deviation = 1
Perform reliability calculations#
We perform the reliability calculations using the form method.
[5]:
project.settings.reliability_method = ReliabilityMethod.form
project.settings.relaxation_factor = 0.15
project.settings.maximum_iterations = 50
project.settings.epsilon_beta = 0.01
project.run()
project.design_point.print()
Reliability (FORM)
Reliability index = 0.2804
Probability of failure = 0.3896
Convergence = 0.00941 (converged)
Model runs = 1904
Alpha values:
const_val: alpha = 0, x = 1.9
a[0]: alpha = 0.1176, x = -0.02631
a[1]: alpha = 0.1176, x = -0.02631
a[2]: alpha = 0.1176, x = -0.02631
a[3]: alpha = 0.1176, x = -0.02631
a[4]: alpha = 0.1176, x = -0.02631
a[5]: alpha = 0.1176, x = -0.02631
a[6]: alpha = 0.1176, x = -0.02631
a[7]: alpha = 0.1176, x = -0.02631
a[8]: alpha = 0.1176, x = -0.02631
a[9]: alpha = 0.1176, x = -0.02631
a[10]: alpha = 0.1176, x = -0.02631
a[11]: alpha = 0.1176, x = -0.02631
a[12]: alpha = 0.1176, x = -0.02631
a[13]: alpha = 0.1176, x = -0.02631
a[14]: alpha = 0.1176, x = -0.02631
a[15]: alpha = 0.1176, x = -0.02631
a[16]: alpha = 0.1176, x = -0.02631
a[17]: alpha = 0.1176, x = -0.02631
a[18]: alpha = 0.1176, x = -0.02631
a[19]: alpha = 0.1176, x = -0.02631
a[20]: alpha = 0.1176, x = -0.02631
a[21]: alpha = 0.1176, x = -0.02631
a[22]: alpha = 0.1176, x = -0.02631
a[23]: alpha = 0.1176, x = -0.02631
a[24]: alpha = 0.1176, x = -0.02631
b[0]: alpha = 0.1477, x = -0.04141
b[1]: alpha = 0.1477, x = -0.04141
b[2]: alpha = 0.1477, x = -0.04141
b[3]: alpha = 0.1477, x = -0.04141
b[4]: alpha = 0.1477, x = -0.04141
b[5]: alpha = 0.1477, x = -0.04141
b[6]: alpha = 0.1477, x = -0.04141
b[7]: alpha = 0.1477, x = -0.04141
b[8]: alpha = 0.1477, x = -0.04141
b[9]: alpha = 0.1477, x = -0.04141
b[10]: alpha = 0.1477, x = -0.04141
b[11]: alpha = 0.1477, x = -0.04141
b[12]: alpha = 0.1477, x = -0.04141
b[13]: alpha = 0.1477, x = -0.04141
b[14]: alpha = 0.1477, x = -0.04141
b[15]: alpha = 0.1477, x = -0.04141
b[16]: alpha = 0.1477, x = -0.04141
b[17]: alpha = 0.1477, x = -0.04141
b[18]: alpha = 0.1477, x = -0.04141
b[19]: alpha = 0.1477, x = -0.04141
b[20]: alpha = 0.1477, x = -0.04141
b[21]: alpha = 0.1477, x = -0.04141
b[22]: alpha = 0.1477, x = -0.04141
b[23]: alpha = 0.1477, x = -0.04141
b[24]: alpha = 0.1477, x = -0.04141
b[25]: alpha = 0.1477, x = -0.04141
b[26]: alpha = 0.1477, x = -0.04141
b[27]: alpha = 0.1477, x = -0.04141
b[28]: alpha = 0.1477, x = -0.04141
b[29]: alpha = 0.1477, x = -0.04141
Similar distributions#
It can also occur that variables in the array follow a similar distribution, which can be defined, for example, using a formula. This is demonstrated for the array \(a\):
[ ]:
for i in range(project.variables["a"].array_size):
a_array = Stochast()
a_array.distribution = DistributionType.normal
a_array.location = 1.0
a_array.scale = 1.0+0.1*i
project.variables["a"].array_variables.append(a_array)
project.run()
project.design_point.print()
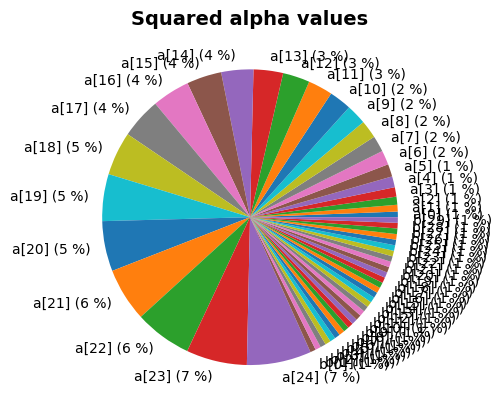
project.design_point.plot_alphas()
Reliability (FORM)
Reliability index = 2.101
Probability of failure = 0.01784
Convergence = 0.009844 (converged)
Model runs = 1904
Alpha values:
const_val: alpha = 0, x = 1.9
a[0]: alpha = 0.07809, x = 0.836
a[1]: alpha = 0.0859, x = 0.8015
a[2]: alpha = 0.0937, x = 0.7638
a[3]: alpha = 0.1015, x = 0.7228
a[4]: alpha = 0.1093, x = 0.6785
a[5]: alpha = 0.1171, x = 0.6309
a[6]: alpha = 0.1249, x = 0.5801
a[7]: alpha = 0.1327, x = 0.526
a[8]: alpha = 0.1406, x = 0.4686
a[9]: alpha = 0.1484, x = 0.4079
a[10]: alpha = 0.1562, x = 0.3439
a[11]: alpha = 0.164, x = 0.2767
a[12]: alpha = 0.1718, x = 0.2061
a[13]: alpha = 0.1796, x = 0.1323
a[14]: alpha = 0.1874, x = 0.05522
a[15]: alpha = 0.1952, x = -0.02515
a[16]: alpha = 0.203, x = -0.1088
a[17]: alpha = 0.2108, x = -0.1957
a[18]: alpha = 0.2186, x = -0.286
a[19]: alpha = 0.2265, x = -0.3794
a[20]: alpha = 0.2343, x = -0.4762
a[21]: alpha = 0.2421, x = -0.5763
a[22]: alpha = 0.2499, x = -0.6796
a[23]: alpha = 0.2577, x = -0.7862
a[24]: alpha = 0.2655, x = -0.8961
b[0]: alpha = 0.07809, x = -0.164
b[1]: alpha = 0.07809, x = -0.164
b[2]: alpha = 0.07809, x = -0.164
b[3]: alpha = 0.07809, x = -0.164
b[4]: alpha = 0.07809, x = -0.164
b[5]: alpha = 0.07809, x = -0.164
b[6]: alpha = 0.07809, x = -0.164
b[7]: alpha = 0.07809, x = -0.164
b[8]: alpha = 0.07809, x = -0.164
b[9]: alpha = 0.07809, x = -0.164
b[10]: alpha = 0.07809, x = -0.164
b[11]: alpha = 0.07809, x = -0.164
b[12]: alpha = 0.07809, x = -0.164
b[13]: alpha = 0.07809, x = -0.164
b[14]: alpha = 0.07809, x = -0.164
b[15]: alpha = 0.07809, x = -0.164
b[16]: alpha = 0.07809, x = -0.164
b[17]: alpha = 0.07809, x = -0.164
b[18]: alpha = 0.07809, x = -0.164
b[19]: alpha = 0.07809, x = -0.164
b[20]: alpha = 0.07809, x = -0.164
b[21]: alpha = 0.07809, x = -0.164
b[22]: alpha = 0.07809, x = -0.164
b[23]: alpha = 0.07809, x = -0.164
b[24]: alpha = 0.07809, x = -0.164
b[25]: alpha = 0.07809, x = -0.164
b[26]: alpha = 0.07809, x = -0.164
b[27]: alpha = 0.07809, x = -0.164
b[28]: alpha = 0.07809, x = -0.164
b[29]: alpha = 0.07809, x = -0.164