Fitting with prior distribution

In this example, we demonstrate how to update the prior distribution with data to obtain a posterior distribution. The main assumption is that the posterior distribution belongs to the same probability distribution family as the prior. In that case, the prior and posterior are called conjugate distributions.

This functionality supports three distribution types: normal, log_normal and bernoulli.

We begin by importing the required classes:

from probabilistic_library import Stochast, DistributionType

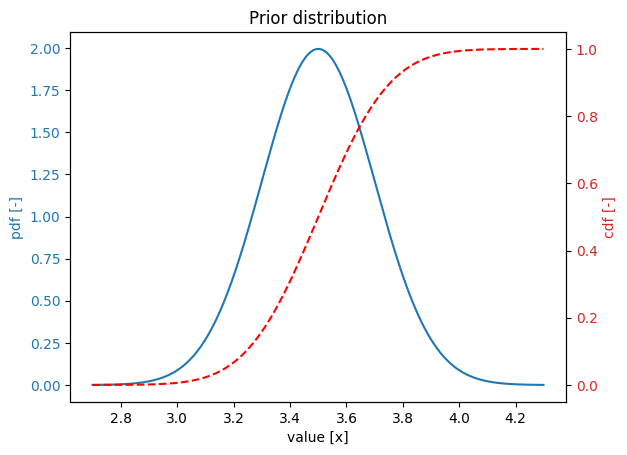
Define prior

We define the prior distribution:

prior = Stochast()
prior.distribution = DistributionType.normal
prior.mean = 3.5
prior.deviation = 0.2

plt = prior.get_plot()
plt.title("Prior distribution")

Text(0.5, 1.0, 'Prior distribution')

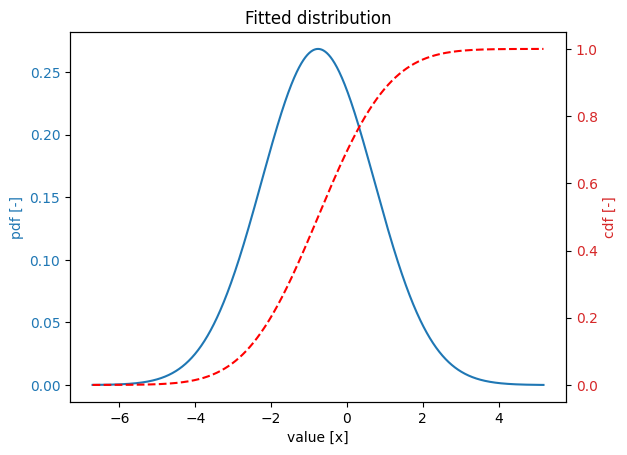
Fit distribution

Suppose we have a set of observations, and we fit a distribution to these data. The distribution must be of the same type as the prior distribution:

data = [-0.1, 0.0, -0.2, -4.0, -0.1, 0.1, 0.2, -2.0]

variable = Stochast()
variable.distribution = DistributionType.normal
variable.fit(data)

variable.print()
plt = variable.get_plot()
plt.title("Fitted distribution")

Variable:
  distribution = normal
Definition:
  location = -0.7625
  scale = 1.486
Derived values:
  mean = -0.7625
  deviation = 1.486
  variation = 1.949

Text(0.5, 1.0, 'Fitted distribution')

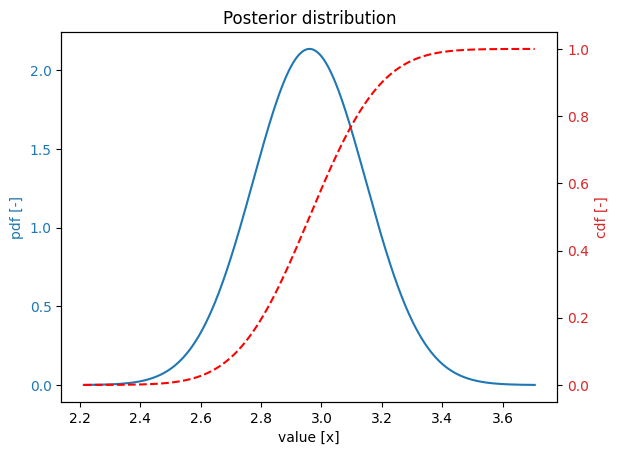
Derive posterior

Then, we derive the posterior distribution using the fit_prior() method:

variable.fit_prior(prior, data)

variable.print()
plt = variable.get_plot()
plt.title("Posterior distribution")
plt.show()

Variable:
  distribution = normal
Definition:
  location = 2.961
  scale = 0.1869
Derived values:
  mean = 2.961
  deviation = 0.1869
  variation = 0.06314

Text(0.5, 1.0, 'Posterior distribution')