FORM and correlations

Reliability calculations with FORM

In this example, we will demonstrate how to perform reliability calculations using the First Order Reliability Method (FORM).

Define model

First, let’s import the necessary classes:

from probabilistic_library import ReliabilityProject, DistributionType, ReliabilityMethod, StartMethod

Next, we define a simple limit state function:

\(Z = 1.9 - (a+b)\)

This is a linear model involving two variables, \(a\) and \(b\).

from utils.models import linear_a_b

To perform a reliability analysis, we create a reliability project and specify the limit state function (model):

project = ReliabilityProject()
project.model = linear_a_b

project.model.print()

Model linear_a_b:
Input parameters:
  a
  b
Output parameters:
  Z

We assume that variables \(a\) and \(b\) are uniformly distributed over the interval \([-1, 1]\). This is defined as follows:

project.variables["a"].distribution = DistributionType.uniform
project.variables["a"].minimum = -1
project.variables["a"].maximum = 1

project.variables["b"].distribution = DistributionType.uniform
project.variables["b"].minimum = -1
project.variables["b"].maximum = 1

Define reliability method

We use the reliability method form. We choose the calculation settings: relaxation_factor, maximum_iterations and epsilon_beta.

project.settings.reliability_method = ReliabilityMethod.form
project.settings.relaxation_factor = 0.15
project.settings.maximum_iterations = 50
project.settings.epsilon_beta = 0.01

We can also define the start method, with the following options available: ray_search, one, fixed_value, sensitivity_search, and sphere_search. If the fixed_value option is selected, a start value must be specified for each variable.

# fixed_value
project.settings.start_method = StartMethod.fixed_value
project.settings.stochast_settings["a"].start_value = 1.2
project.settings.stochast_settings["b"].start_value = 2.4

# in this example we choose the ray_search method
project.settings.start_method = StartMethod.ray_search

Perform calculations

We use project.run() to execute the reliability analysis:

project.run()

The results are written to project.design_point and consist of:

• reliability index \(\beta\)

• failure probability \(P_f\)

• influence coefficients \(\alpha\)-values

• design point \(x\)-values

• information about the convergence of FORM

project.design_point.print()
project.design_point.plot_alphas()

Reliability (FORM)
 Reliability index = 2.773
 Probability of failure = 0.0028
 Convergence = 0.0088 (converged)
 Model runs = 54
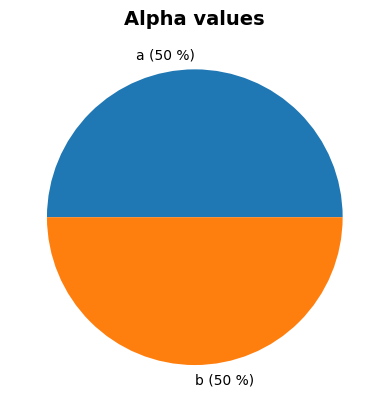
Alpha values:
 a: alpha = -0.7071, x = 0.9501
 b: alpha = -0.7071, x = 0.9501

Contributing design points:
  Reliability (Start point)
   Reliability index = 3.6937
   Probability of failure = 1.104871e-04
   Model runs = 11
  Alpha values:
   a: alpha = -0.4472, x = 0.9014
   b: alpha = -0.8944, x = 0.999

Correlated variables

In the above example, variables \(a\) and \(b\) are independent. However, it is also possible to introduce a correlation between \(a\) and \(b\). The example below demonstrates this with a partial correlation coefficient of \(0.8\).

project.correlation_matrix["a", "b"] = 0.8
project.run()

project.design_point.print()
project.design_point.plot_alphas()

Reliability (FORM)
 Reliability index = 2.0646
 Probability of failure = 0.0195
 Convergence = 0.0084 (converged)
 Model runs = 39
Alpha values:
 a: alpha = -0.9565, x = 0.9517
 b: alpha = -0.2916, x = 0.9478

Contributing design points:
  Reliability (Start point)
   Reliability index = 3.6937
   Probability of failure = 1.104871e-04
   Model runs = 11
  Alpha values:
   a: alpha = -0.4472, x = 0.9014
   b: alpha = -0.8944, x = 0.999