Example: Doing Extreme Value Analysis (EVA) for time series#

This example illustrates how to use to perform Extreme Value Analysis (EVA) based on time series stored in a netcdf, for example, this could be performed on a xarray Dataset. Typical steps needed to perform EVA are: - extract peaks (high extremes) from a continuous time series - fit a EV distribution on these peaks - obtain return values for given return periods based on the distribution fitted and its parameters - plot the distribution and empirical data

All these steps are also combined in the function eva (see also the end of the example)

We cover these steps in this example using randomly generated data. More details on the functions used can be found in the API reference description of the Statistics and Extreme Value Analysis

Note that here are also other packages for extreme valua analysis.

scipy.stats Library of many statistical distributions including extreme value distributions.
pyextremes Very rich package for univariate extreme value analysis with many different fitting methods, builds on scipy.stats.

Compared to these packages The HydroMT methods add the following features, but is generally much less feature rich: - support for performing extreme valua analysis on ND Xarray Datasets - support for lmoments fitting

[1]:

# import hydromt and functions needed for EVA
from hydromt.stats import extremes
import xarray as xr
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

We load a random discharge time seriesaas a xarray DataArray da for two stations (stations 1 and 2).

[2]:

# We create some random continuous time series with some extremes
da = xr.open_dataarray(r"./data/discharge.nc")
da

Extreme value distribution fit is based either on block maxima (BM) or peaks-over-threshold (PoT).

If sampling of high extremes is done according to BM then, distributions to be fit are either Gumbel (later referred as gumb) or the Generalized Extreme Value (GEV) distribution (later referred as gev). Note that a GEV distribution with a shape paramater of 0 is equivalent to the Gumbel distribution.
If sampling of high extremes is done according to PoT then, distributions to be fit are either exponential (later referred as exp) or the Generalized Pareto (GP) distribution (later referred as gpd).

For this example, we will fit a GEV distribution based on annual maxima.

Step 1: Extracting peaks from continuous time series#

[3]:

# We use the get_peaks function
bm_peaks = extremes.get_peaks(da, ev_type="BM", period="365.25D")

fig, ax = plt.subplots(figsize=(10, 3))
da.to_pandas().plot(
    ax=ax, xlabel="time", ylabel="discharge [m3/s]", color=["orange", "green"]
)
bm_peaks.to_pandas().plot(
    ax=ax,
    marker="o",
    linestyle="none",
    legend=False,
    color=["darkorange", "darkgreen"],
    markersize=4,
)

[3]:

<Axes: xlabel='time', ylabel='discharge [m3/s]'>

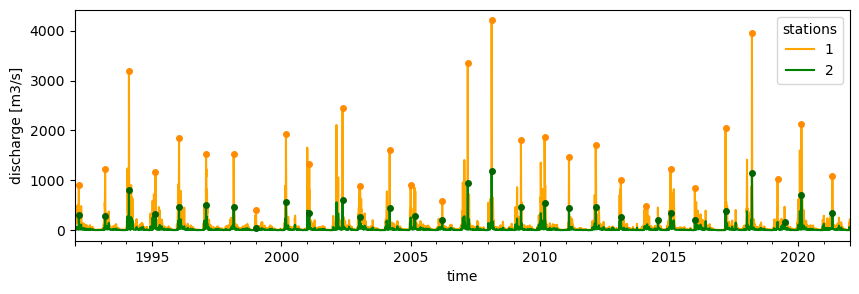
../_images/_examples_doing_extreme_value_analysis_8_1.png

The function extracts peaks, here, annual maxima, and set the rest of the time series to NaN. Here, the extremes_rate is equal to 1 as we have sampled the highest value per year.

Step 3: obtain return values for given return periods based on the distribution fitted and its parameters#

[5]:

# We define the return periods for which we would like to know the return values
rps = np.array([2, 5, 25, 100, 500])
da_rps = extremes.get_return_value(da_params, rps=rps).load()
da_rps.to_pandas()

[5]:

rps	2	5	25	100	500
stations
1	1425.770861	2252.428221	3773.468116	5341.066751	7584.131635
2	389.952957	621.148509	1056.736145	1517.185877	2192.705849

Step 4: plot the distribution and empirical data#

[6]:

# We plot the fit obtained using the function plot_return_values!

fig, axes = plt.subplots(2, 1, figsize=(5, 7), sharex=True)

for i, ax, color in zip(da.stations.values, axes, ["orange", "green"]):
    extremes.plot_return_values(
        bm_peaks.sel(stations=i),
        da_params.sel(stations=i),
        "gev",
        color=color,
        nsample=1000,  # number of samples for confidence interval
        rps=rps,
        extremes_rate=1.0,
        ax=ax,
    )
    ax.set_title(f"Station {i}")
    ax.set_ylabel("discharge [m3/s]")
    if i == da.stations.values[-1]:
        ax.set_xlabel("return period [years]")
    else:
        ax.set_xlabel("")

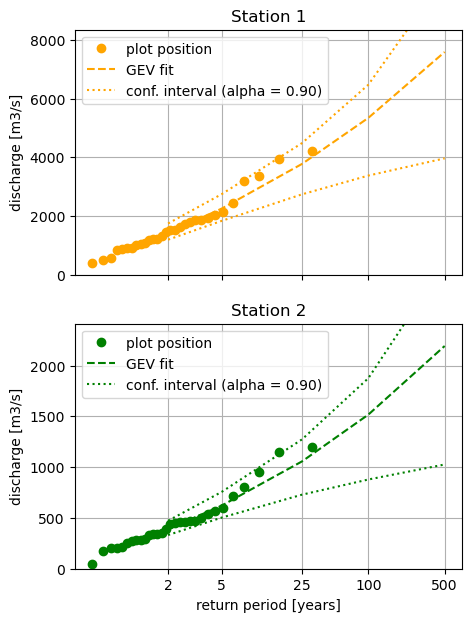
../_images/_examples_doing_extreme_value_analysis_15_0.png

Example: Doing Extreme Value Analysis (EVA) for time series#

Step 1: Extracting peaks from continuous time series#

Step 2: fit a EV distribution on these peaks#

Step 3: obtain return values for given return periods based on the distribution fitted and its parameters#

Step 4: plot the distribution and empirical data#

TL;DR#