Reservoirs and Lakes
Simplified reservoirs and lakes models can be included as part of the river network.
Reservoirs
Simple reservoirs can be included within the river routing by supplying the following reservoir parameters:
locs- Outlet of the reservoirs in which each reservoir has a unique idarea- Surface area of the reservoirs [m$^2$]areas- Reservoir coveragetargetfullfrac- Target fraction full (of max storage) for the reservoir: number between 0 and 1targetminfrac- Target minimum full fraction (of max storage). Number between 0 and 1maxvolume- Maximum reservoir storage (above which water is spilled) [m$^3$]demand- Minimum (environmental) flow requirement downstream of the reservoir [m$^3$ s$^{-1}$]maxrelease- Maximum Q that can be released if below spillway [m$^3$ s$^{-1}$]
By default the reservoirs are not included in the model. To include them put the following lines in the TOML file of the model:
[model]
reservoirs = trueFinally there is a mapping required between external and internal parameter names in the TOML file, with below an example:
[input]
[input.lateral.river.reservoir]
area = "ResSimpleArea"
areas = "wflow_reservoirareas"
demand = "ResDemand"
locs = "wflow_reservoirlocs"
maxrelease = "ResMaxRelease"
maxvolume = "ResMaxVolume"
targetfullfrac = "ResTargetFullFrac"
targetminfrac = "ResTargetMinFrac"Lakes (unregulated and regulated)
Lakes are modelled using a mass balance approach:
\[ \dfrac{S(t + \Delta t)}{\Delta t} = \dfrac{S(t)}{\Delta t} + Q_{in} + \dfrac{(P-E) A}{\Delta t} - Q_{out}\]
where $S$ is lake storage [m$^3$], $\Delta t$ is the model timestep [s], $Q_{in}$ is the sum of inflows (river, overland and lateral subsurface flow) [m$^3$ s$^{-1}$], $Q_{out}$ is the lake outflow at the outlet [m$^3$ s$^{-1}$], $P$ is precipitation [m], $E$ is lake evaporation [m] and $A$ is the lake surface area [m$^2$].
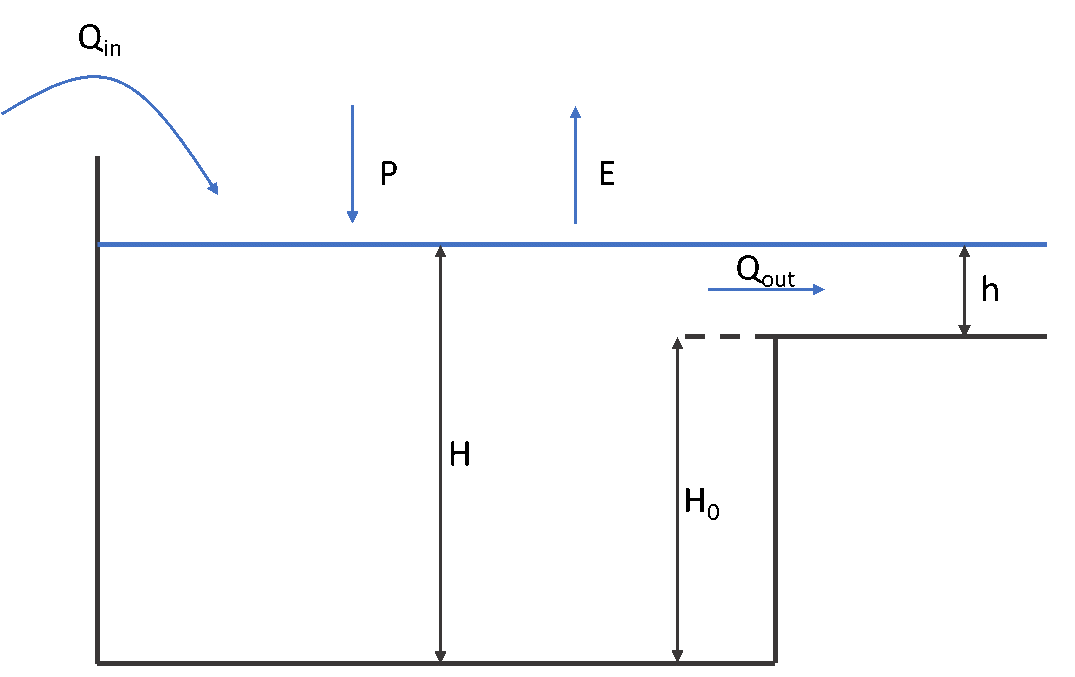
Lake schematization.
Most of the variables in this equation are already known or coming from previous timestep, apart from $S(t+ \Delta t)$ and $Q_{out}$ which can both be linked to the water level $H$ in the lake using a storage curve $S = f(H)$ and a rating curve $Q = f(H)$. In wflow, several options are available to select storage and rating curves, and in most cases, the mass balance is then solved by linearization and iteration or using the Modified Puls Approach from Maniak (Burek et al., 2013). Storage curves in wflow can either:
- Come from the interpolation of field data linking volume and lake height,
- Be computed from the simple relationship $S = A H$.
Rating curves in wflow can either:
- Come from the interpolation of field data linking lake outflow and water height, also appropriate for regulated lakes/ dams,
- Be computed from a rating curve of the form $Q_{out} = \alpha {(H-H_{0})}^{\beta}$, where $H_{0}$ is the minimum water level under which the outflow is zero. Usual values for $\beta$ are 3/2 for a rectangular weir or 2 for a parabolic weir (Bos, 1989).
Modified Puls Approach
The Modified Puls Approach is a resolution method of the lake balance that uses an explicit relationship between storage and outflow. Storage is assumed to be equal to $A H$ and the rating curve for a parabolic weir ($\beta = 2$):
\[ S = A H = A (h + H_{0}) = \dfrac{A}{\sqrt{\alpha}} \sqrt{Q} + A H_{0}\]
Inserting this equation in the mass balance gives:
\[ \dfrac{A}{\Delta t \sqrt{\alpha}} \sqrt{Q} + Q = \dfrac{S(t)}{\Delta t} + Q_{in} + \dfrac{(P-E) A}{\Delta t} - \dfrac{A H_{0}}{\Delta t} = SI - \dfrac{A H_{0}}{\Delta t}\]
The solution for Q is then:
\[ Q = { \left( \dfrac{-LF + \sqrt{LF^{2} + 4 \left( SI - \dfrac{A*H_{0}}{\Delta t} \right)}} {2} \right) }^{2} \text{for } SI > \dfrac{A H_{0}}{\Delta t} \text{ and where}\\ LF = \dfrac{A}{\Delta t \sqrt{\alpha}} \\~\\ Q = 0 \text{ for } SI \leq \dfrac{A*H_{0}}{\Delta t}\]
Lake parameters
Lakes can be included within the kinematic wave river routing in wflow, by supplying the following parameters:
area- Surface area of the lakes [m$^2$]areas- Coverage of the lakeslocs- Outlet of the lakes in which each lake has a unique idlinkedlakelocs- Outlet of linked (downstream) lakes (unique id)waterlevel- Lake water level [m], used to reinitiate lake modelthreshold- Water level threshold $H_{0}$ under which outflow is zero [m]storfunc- Type of lake storage curve ; 1 for $S = AH$ (default) and 2 for $S = f(H)$ from lake data and interpolationoutflowfunc- Type of lake rating curve ; 1 for $Q = f(H)$ from lake data and interpolation, 2 for general $Q = b(H - H_{0})^{e}$ and 3 in the case of Puls Approach $Q = b(H - H_{0})^{2}$ (default)b- Rating curve coefficiente- Rating curve exponent
By default, the lakes are not included in the model. To include them, put the following line in the TOML file of the model:
[model]
lakes = trueThere is also a mapping required between external and internal parameter names in the TOML file, with below an example:
[input]
[input.lateral.river.lake]
area = "lake_area"
areas = "wflow_lakeareas"
b = "lake_b"
e = "lake_e"
locs = "wflow_lakelocs"
outflowfunc = "lake_outflowfunc"
storfunc = "lake_storfunc"
threshold = "lake_threshold"
waterlevel = "lake_waterlevel"Additional settings
Storage and rating curves from field measurement can be supplied to wflow via CSV files supplied in the same folder of the TOML file. Naming of the files uses the ID of the lakes where data are available and is of the form lake_sh_1.csv and lake_hq_1.csv for respectively the storage and rating curves of lake with ID 1.
The storage curve is stored in a CSV file with lake level [m] in the first column H and corresponding lake storage [m $^{3}$] in the second column S:
H, S
392.21, 0
393.21, 430202000
393.71, 649959000
394.21, 869719000The rating curve uses level and discharge data depending on the Julian day of the year (JDOY), and can be also used for regulated lakes/ dams. The first line contains H for the first column. The other lines contain the water level and the corresponding discharges for the different JDOY (1-365), see also the example below, that shows part of a CSV file (first 4 Julian days). The volume above the maximum water level of the rating curve is assumed to flow instantaneously out of the lake (overflow).
H
394, 43, 43, 43, 43
394.01, 44.838, 44.838, 44.838, 44.838
394.02, 46.671, 46.671, 46.671, 46.671
394.03, 48.509, 48.509, 48.509, 48.509
394.04, 50.347, 50.347, 50.347, 50.347
394.05, 52.179, 52.179, 52.179, 52.179Linked lakes: In some cases, lakes can be linked and return flow can be allowed from the downstream to the upstream lake. The linked lakes are defined in the linkedlakelocs parameter that represent the downstream lake location ID, at the grid cell of the upstream lake location.
In every file, level units are meters [m] above lake bottom and not meters above sea level [m asl]. Especially with storage/rating curves coming from data, please be careful and convert units if needed.
References
- Bos M.G., 1989. Discharge measurement structures. Third revised edition, International Institute for Land Reclamation and Improvement ILRI, Wageningen, The Netherlands.
- Burek P., Van der Knijf J.M., Ad de Roo, 2013. LISFLOOD – Distributed Water Balance and flood Simulation Model – Revised User Manual. DOI: http://dx.doi.org/10.2788/24719.