Local inertial
River and floodplain routing
The local inertial approximation of shallow water flow neglects only the convective acceleration term in the Saint-Venant momentum conservation equation. The numerical solution of the local inertial approximation on a staggered grid is as follows (Bates et al., 2010):
\[Q_{t+\Delta t} = \frac{Q_t - g A_t \Delta t S_t}{(1+g\Delta t n^2 |Q_t| / (R_t^{4/3} A_t))}\]
where $Q_{t+\Delta t}$ is the river flow [m$^3$/s] at time step $t+\Delta t$, $g$ is acceleration due to gravity [m/s$^2$], $A_t$ is the cross sectional flow area at the previous time step, $R_t$ is the hydraulic radius at the previous time step, $Q_t$ is the river flow [m$^3$/s] at the previous time step, $S_t$ is the water surface slope at the previous time step and $n$ is the Manning's roughness coefficient [m$^{-1/3}$ s].
The momentum equation is applied to each link between two river grid cells, while the continuity equation over $\Delta t$ is applied to each river cell:
\[h^{t+\Delta t} = h^t + \Delta t \frac{Q^{t+\Delta t}_{src} - Q^{t+\Delta t}_{dst}}{A}\]
where $h^{t+\Delta t}$ is the water depth [m] at time step $t+\Delta t$, $h^t$ is the water depth [m] at the previous time step, $A$ is the river area [m$^2$] and $Q_{src}$ and $Q_{dst}$ represent river flow [m$^3$/s] at the upstream and downstream link of the river cell, respectively.
The model time step $\Delta t$ for the local inertial model is estimated based on the Courant-Friedrichs-Lewy condition (Bates et al., 2010):
\[\Delta t = min(\alpha \frac{\Delta x_i}{\sqrt{(gh_i)}})\]
where $\sqrt{(gh_i)}$ is the wave celerity for river cell $i$ , $\Delta x_i$ is the river length [m] for river cell $i$ and $\alpha$ is a coefficient (typically between 0.2 and 0.7) to enhance the stability of the simulation.
In the TOML file the following properties related to the local inertial model can be provided for the sbm and sbm_gwf model types:
[model]
river_routing = "local-inertial" # default is "kinematic-wave"
inertial_flow_alpha = 0.5 # alpha coefficient for model stability (default = 0.7)
froude_limit = true # default is true, limit flow to subcritical-critical according to Froude number
h_thresh = 0.1 # water depth [m] threshold for calculating flow between cells (default = 1e-03)
floodplain_1d = true # include 1D floodplain schematization (default = false)Two optional constant boundary conditions riverlength_bc and riverdepth_bc can be provided at a river outlet node (or multiple river outlet nodes) through the model parameter netCDF file, as follows:
[input.lateral.river]
riverlength_bc = "riverlength_bc" # optional river length [m], default = 1e04
riverdepth_bc = "riverdepth_bc" # optional river depth [m], default = 0.0These boundary conditions are copied to a ghost node (downstream of the river outlet node) in the code.
The optional 1D floodplain schematization is based on provided flood volumes as a function of flood depth (per flood depth interval) for each river cell. Wflow calculates from these flood volumes a rectangular floodplain profile for each flood depth interval. Routing is done separately for the river channel and floodplain.
The momentum equation is most stable for low slope environments, and to keep the simulation stable for (partly) steep environments the froude_limit option is set to true by default. This setting limits flow conditions to subcritical-critical conditions based on the Froude number ($\le 1$), similar to Coulthard et al. (2013) in the CAESAR-LISFLOOD model and Adams et al. (2017) in the Landlab v1.0 OverlandFlow component. The froude number $Fr$ on a link is calculated as follows:
\[ Fr = \frac{u}{\sqrt{(gh_f)}}\]
where $\sqrt{(gh_f)}$ is the wave celerity on a link and $u$ is the water velocity on a link. If the water velocity from the local inertial model is causing the Froude number to be greater than 1.0, the water velocity (and flow) is reduced in order to maintain a Froude number of 1.0.
The downstream boundary condition basically simulates a zero water depth boundary condition at a set distance, as follows. For the downstream boundary condition (ghost point) the river width, river bed elevation and Manning's roughness coefficient are copied from the upstream river cell. The river length [m] of the boundary cell can be set through the TOML file with riverlength_bc, and has a default value of 10 km. The water depth at the boundary cell is fixed at 0.0 m.
Simplified reservoir and lake models can be included as part of the local inertial model for river flow (1D) and river and overland flow combined (see next section). Reservoir and lake models are included as a boundary point with zero water depth for both river and overland flow. For river flow the reservoir or lake model replaces the local inertial model at the reservoir or lake location, and $Q$ is set by the outflow from the reservoir or lake. Overland flow at a reservoir or lake location is not allowed to or from the downstream river grid cell.
Overland flow (2D)
For the simulation of 2D overland flow on a staggered grid the numerical scheme proposed by de Almeida et al. (2012) is adopted. The explicit solution for the estimation of water discharge between two cells in the x-direction is of the following form (following the notation of Almeida et al. (2012)):
\[Q_{i-1/2}^{n+1} = \frac{\left[ \theta Q_{i-1/2}^{n} +\frac{(1-\theta)}{2}(Q_{(i-3/2)}^{n} + \\ Q_{(i+1/2)}^{n})\right]- g h_f \frac{\Delta t}{\Delta x} (\eta^n_i - \eta^n_{i-1}) \Delta y}{1+g\Delta t \\ n^2 |Q_{i-1/2}^{n}|/(h_f^{7/3} \Delta y)}\]
where subscripts $i$ and $n$ refer to space and time indices, respectively. Subscript $i-1/2$ is to the link between node $i$ and $i-1$, subscript $i+1/2$ is the link between node $i$ and node $i+1$, and subscript $i-3/2$ is the link between node $i-1$ and node $i-2$. $Q$ is the water discharge [m$^3$ s$^{-1}$], $\eta$ is the water surface elevation [m], $h_f$ [m] is the water depth between cells, $n$ is the Manning's roughness coefficient [m$^{-1/3}$ s], $g$ is acceleration due to gravity [m/s$^2$], $\Delta t$ [s] is the adaptive model time step, $\Delta x$ [m] is the distance between two cells and $\Delta y$ [m] is the flow width. Below the staggered grid and variables of the numerical solution in the x-direction, based on Almeida et al. (2012):
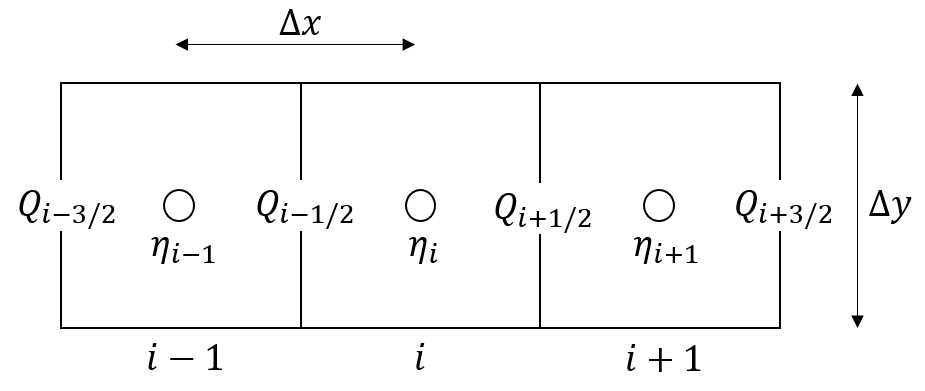
The overland flow local inertial approach is used in combination with the local inertial river routing. This is a similar to the modelling approach of Neal et al. (2012), where the hydraulic model LISFLOOD-FP was extended with a subgrid channel model. For the subgrid channel, Neal et al. (2012) make use of a D4 (four direction) scheme, while here a D8 (eight direction) scheme is used, in combination with the D4 scheme for 2D overland flow.
In the TOML file the following properties related to the local inertial model with 1D river routing and 2D overland flow can be provided for the sbm model type:
[model]
land_routing = "local-inertial" # default is kinematic-wave
river_routing = "local-inertial" # default is kinematic-wave
inertial_flow_alpha = 0.5 # alpha coefficient for model stability (default = 0.7)
froude_limit = true # default is true, limit flow to subcritical-critical according to Froude number
h_thresh = 0.1 # water depth [m] threshold for calculating flow between cells (default = 1e-03)The properties inertial_flow_alpha, froude_limit and h_thresh apply to 1D river routing as well as 2D overland flow. The properties inertial_flow_alpha and froude_limit, and the adaptive model time step $\Delta t$ are explained in more detail in the River and floodplain routing section of the local inertial model.
Inflow
External water (supply/abstraction) inflow [m$^3$ s$^{-1}$] can be added to the local inertial model for river flow (1D) and river and overland flow combined (1D-2D), as a cyclic parameter or as part of forcing (see also Input section).
Abstractions
Abstractions from the river through the variable abstraction [m$^3$ s${-1}$] are possible when water demand and allocation is computed. The variable abstraction is set from the water demand and allocation module each time step. Abstractions are subtracted as part of the continuity equation of the local inertial model.
Multi-Threading
The local inertial model for river flow (1D) and river and overland flow combined (1D-2D) can be executed in parallel using multiple threads.
References
- Adams, J. M., Gasparini, N. M., Hobley, D. E. J., Tucker, G. E., Hutton, E. W. H., Nudurupati, S. S., and Istanbulluoglu, E., 2017, The Landlab v1.0 OverlandFlow component: a Python tool for computing shallow-water flow across watersheds, Geosci. Model Dev., 10, 1645–1663, https://doi.org/10.5194/gmd-10-1645-2017.
- de Almeida, G. A. M., P. Bates, J. E. Freer, and M. Souvignet, 2012, Improving the stability of a simple formulation of the shallow water equations for 2-D flood modeling, Water Resour. Res., 48, W05528, https://doi.org/10.1029/2011WR011570.
- Bates, P. D., M. S. Horritt, and T. J. Fewtrell, 2010, A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling, J. Hydrol., 387, 33–45, https://doi.org/10.1016/j.jhydrol.2010.03.027.
- Coulthard, T. J., Neal, J. C., Bates, P. D., Ramirez, J., de Almeida, G. A. M., and Hancock, G. R., 2013, Integrating the LISFLOOD-FP 2- D hydrodynamic model with the CAESAR model: implications for modelling landscape evolution, Earth Surf. Proc. Land., 38, 1897–1906, https://doi.org/10.1002/esp.3478.
- Neal, J., G. Schumann, and P. Bates (2012), A subgrid channel model for simulating river hydraulics and floodplaininundation over large and data sparse areas, Water Resour.Res., 48, W11506, https://doi.org/10.1029/2012WR012514.