Mesh2d refinement based on gridded samples

This is a brief introduction to the process of mesh refinement using gridded samples. When refining the mesh using gridded samples, bilinear interpolation is used to calculate the depth values at the mesh nodes.

At the very beginning, the necessary libraries have to be imported.

import matplotlib.pyplot as plt
import numpy as np
from meshkernel import (
    GeometryList,
    GriddedSamples,
    MakeGridParameters,
    MeshKernel,
    MeshRefinementParameters,
    RefinementType,
)

meshkernel provides a set of convenience methods for creating common meshes.

We use the curvilinear_compute_rectangular_grid method to create a simple curvilinear grid. You can look at the documentation in order to find all its parameters.

mk = MeshKernel()

make_grid_parameters = MakeGridParameters()
make_grid_parameters.num_columns = 4
make_grid_parameters.num_rows = 5
make_grid_parameters.angle = 0.0
make_grid_parameters.origin_x = 0.0
make_grid_parameters.origin_y = 0.0
make_grid_parameters.block_size_x = 100.0
make_grid_parameters.block_size_y = 100.0

mk.curvilinear_compute_rectangular_grid(make_grid_parameters)

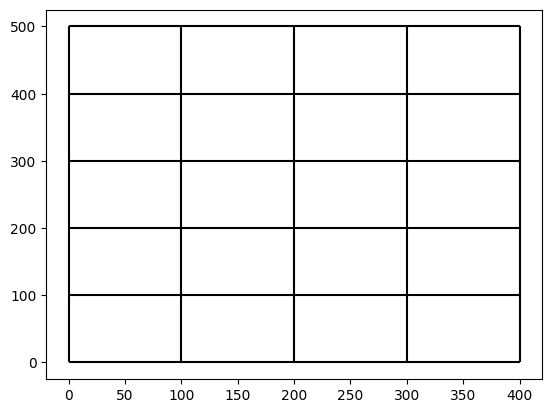
We convert the curvilinear grid to an unstructured mesh and get the resulting mesh2d

mk.curvilinear_convert_to_mesh2d()
mesh2d_input = mk.mesh2d_get()

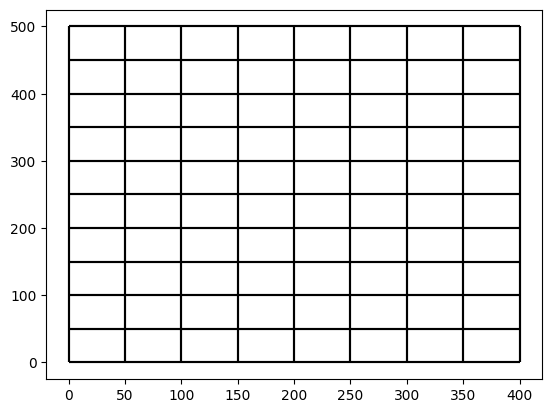
The generated mesh can be visualized as follow

fig, ax = plt.subplots()
mesh2d_input.plot_edges(ax, color="black")

Now we define the gridded samples with uniform spacing

gridded_samples = GriddedSamples(
    num_x=5,
    num_y=6,
    x_origin=-50.0,
    y_origin=-50.0,
    cell_size=100.0,
    values=np.array([-0.05] * 42, dtype=np.float32),
)

And the parameters for the mesh refinement algorithm

refinement_params = MeshRefinementParameters(
    refine_intersected=False,
    use_mass_center_when_refining=False,
    min_edge_size=2.0,
    refinement_type=RefinementType.WAVE_COURANT,
    connect_hanging_nodes=True,
    account_for_samples_outside_face=False,
    max_refinement_iterations=5,
)

Refinement can now be performed

mk.mesh2d_refine_based_on_gridded_samples(gridded_samples, refinement_params, True)

We can now visualize the refined grid

mesh2d_output = mk.mesh2d_get()
fig, ax = plt.subplots()
mesh2d_output.plot_edges(ax, color="black")

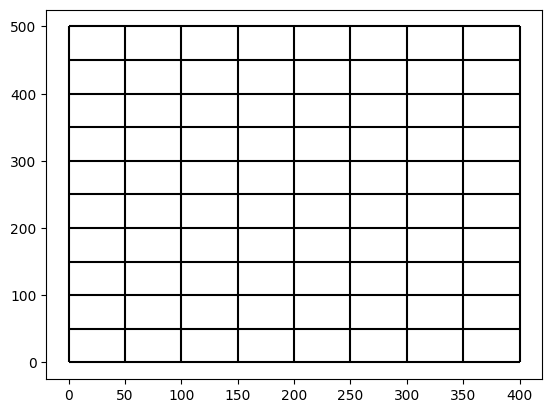
If gridding is not uniform, we can create the gridded samples differently, bmitting some of the GriddedSamples parameters. First regenerate the starting mesh

mk.curvilinear_compute_rectangular_grid(make_grid_parameters)
mk.curvilinear_convert_to_mesh2d()

fig, ax = plt.subplots()
mesh2d_input.plot_edges(ax, color="black")

When refining the mesh with gridded samples that have non-uniform x or y spacing, the non-uniform spacing can be specified by using the x_coordinates and y_coordinates parameters.

gridded_samples = GriddedSamples(
    x_coordinates=np.array([-50.0, 50.0, 150.0, 250.0, 350.0, 450.0], dtype=np.double),
    y_coordinates=np.array(
        [-50.0, 50.0, 150.0, 250.0, 350.0, 450.0, 550.0], dtype=np.double
    ),
    values=np.array([-0.05] * 42, dtype=np.float32),
)

mk.mesh2d_refine_based_on_gridded_samples(gridded_samples, refinement_params, True)

mesh2d_output = mk.mesh2d_get()
fig, ax = plt.subplots()
mesh2d_output.plot_edges(ax, color="black")