Sediment
Over the land, soil erosion, also called soil loss, is closely linked to the water cycle. The main processes governing sediment generation are splash erosion from rain droplets, and sheet and rill erosion from the shear stress caused by overland flow. The intensity of soil erosion by rain or flow depends on the land and soil characteristics such as slope, land use or soil type. Once soil is eroded, the detached particles can be transported downslope by overland flow. Along the transport pathways, soil particles can also be deposited due to a low flow velocity, a change of topography in depressions, footslopes or valley bottoms, and/or can be filtered and stopped by a change in vegetation such as field boundaries.
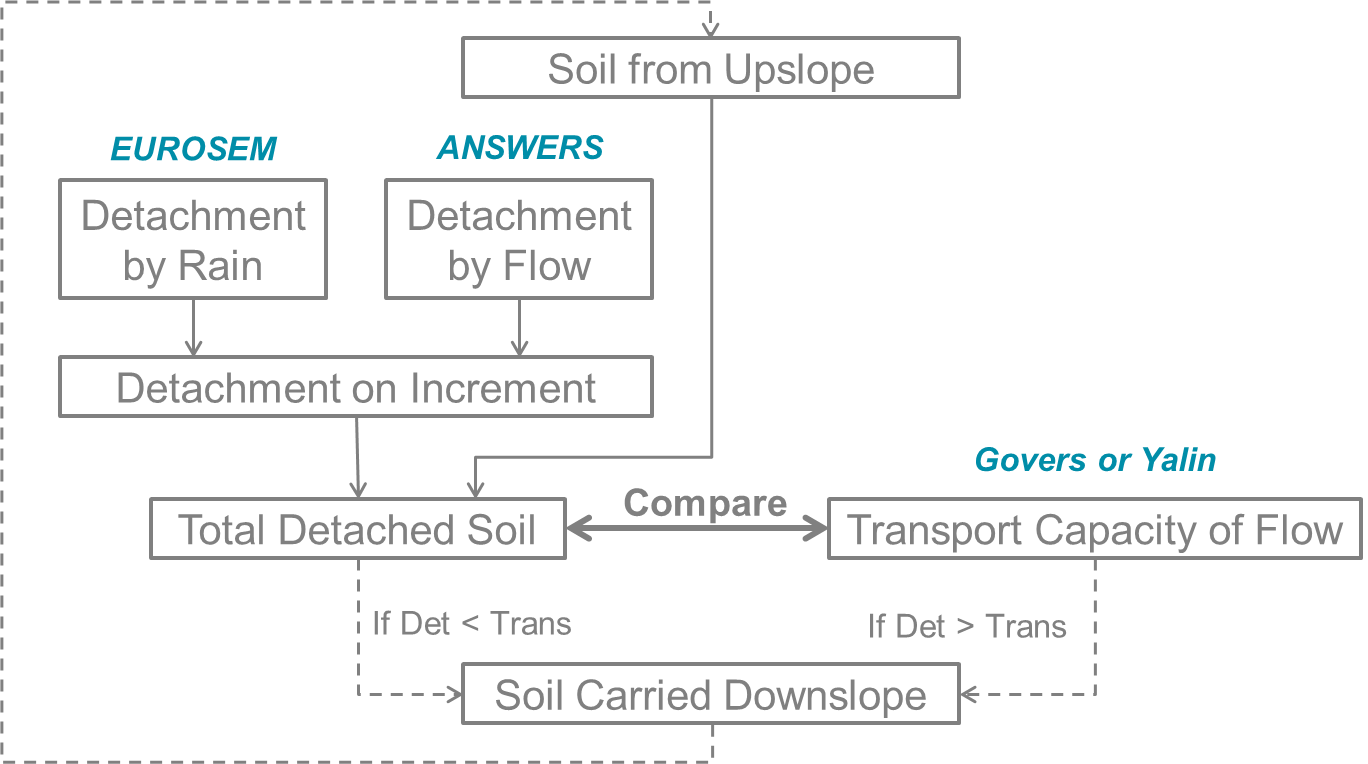
The inland part of the sediment gathers these different processes, separated in a vertical structure for the soil loss and lateral structure for the transport in overland flow.
Soil Erosion
The first process to consider in sediment dynamics is the generation of sediments by land erosion. The main processes behind soil loss are rainfall erosion and overland flow erosion. In order to model such processes at a fine time and space scale, physics-based models such as ANSWERS and EUROSEM were chosen here.
The choice of rainfall erosion method is set up in the model section of the TOML:
[model]
rainerosmethod = "answers" # Rainfall erosion equation: ["answers", "eurosem"]Rainfall erosion
In wflow_sediment, rainfall erosion can both be modelled using EUROSEM or ANSWERS equation. The main difference between the models is that EUROSEM uses a more physics-based approach based on the kinetic energy of the rain drops impacting the soil (Morgan et al, 1998), while ANSWERS is more empirical and uses parameters from the USLE model (Beasley et al, 1991).
In EUROSEM, rainfall erosion is modelled according to rainfall intensity and its kinetic energy when it reaches the soil according to equations developed by Brandt (1990). As the intensity of the rain kinetic energy depends on the length of the fall, rainfall intercepted by vegetation will then be reduced compared to direct throughfall. The kinetic energy of direct throughfall is estimated by (Morgan et al, 1998): \[ \subtext{\mathrm{KE}}{direct} = 8.95 + 8.44\,\log_{10}(R_i) \]
where \(\SIb{\subtext{\mathrm{KE}}{direct}}{J m^{-2} mm^{-1}}\) is the kinetic energy of direct throughfall and \(\SIb{R_i}{mm h^{-1}}\) is rainfall intensity. If the rainfall is intercepted by vegetation and falls as leaf drainage, its kinetic energy is then reduced according to (Brandt, 1990): \[ \subtext{\mathrm{KE}}{leaf} = 15.8\,\sqrt{H_p} - 5.87 \] where \(\SIb{\subtext{\mathrm{KE}}{leaf}}{J m^{-2} mm^{-1}}\) is kinetic energy of leaf drainage and \(\SIb{H_p}{m}\) is the effective canopy height (half of plant height). Canopy height can be derived from the global map from Simard & al. (2011) or by user input depending on the land use.
Kinetic energies from both direct throughfall and leaf drainage are then multiplied by the respective depths of direct throughfall and leaf drainage (mm) and added to get the total rainfall kinetic energy \(\mathrm{KE}\). The soil detached by rainfall \(\SIb{D_R}{g m^{-2}}\) is then: \[
D_R = k\,\mathrm{KE}\,e^{-\varphi h}
\] where \(\SIb{k}{g J^{-1}}\) is an index of the detachability of the soil, \(\SIb{\mathrm{KE}}{J
m^{-2}}\) is the total rainfall kinetic energy, \(\SIb{h}{m}\) is the surface runoff depth on the soil and \(\varphi\) is an exponent varying between \(0.9\) and \(3.1\) used to reduce rainfall impact if the soil is already covered by water. As a simplification, Torri (1987) has shown that a value of \(2.0\) for \(\varphi\) is representative enough for a wide range of soil conditions. The detachability of the soil \(k\) depends on the soil texture (proportion of clay, silt and sand content) and corresponding values are defined in EUROSEM user guide (Morgan et al, 1998). As a simplification, in wflow_sediment, the mean value of the detachability shown in the table below are used. Soil texture can for example be derived from the topsoil clay and silt content from SoilGrids (Hengl et al, 2017).
| Texture (USDA system) | Mean detachability \(\SIb{k}{g J^{-1}}\) |
|---|---|
| Clay | 2.0 |
| Clay Loam | 1.7 |
| Silt | 1.2 |
| Silt Loam | 1.5 |
| Loam | 2.0 |
| Sandy Loam | 2.6 |
| Loamy Sand | 3.0 |
| Fine Sand | 3.5 |
| Sand | 1.9 |
Rainfall erosion is handled differently in ANSWERS. There, the impacts of vegetation and soil properties are handled through the USLE coefficients in the equation (Beasley et al, 1991): \[ D_R = 0.108 \, \subtext{C}{USLE} \, \subtext{K}{USLE} \, A_i \, R_i^2 \] where \(\SIb{D_R}{kg min^{-1}}\) is the soil detachment by rainfall, \(\subtext{C}{USLE}\) is the soil cover-management factor from the USLE equation, \(\subtext{K}{USLE}\) is the soil erodibility factor from the USLE equation, \(\SIb{A_i}{m^2}\) is the area of the cell and \(\SIb{R_i}{mm\;min^{-1}}\) is the rainfall intensity. There are several methods available to estimate the \(C\) and \(K\) factors from the USLE. They can come from user input maps, for example maps resulting from Panagos & al.’s recent studies for Europe (Panagos et al, 2015) (Ballabio et al, 2016). To get an estimate of the \(C\) factor globally, the other method is to estimate \(C\) values for the different land use type in from global land cover maps (e.g. GlobCover). An example is given for the global land cover map GlobCover, summed up in the table below, the values come from a literature study including Panagos et al.’s review (2015), Gericke & al. (2015), Mansoor & al. (2013), Chadli et al. (2016), de Vente et al. (2009), Borrelli et al. (2014), Yang et al. (2003) and Bosco et al. (2015).
The other methods to estimate the USLE \(K\) factor are to use either topsoil composition or topsoil geometric mean diameter. \(K\) estimation from topsoil composition is estimated with the equation developed in the EPIC model (Williams et al, 1983): \[ \begin{gathered} \subtext{K}{USLE} = \left[ 0.2 + 0.3\exp\left(-0.0256\;\mathrm{SAN}\frac{(1-\mathrm{SIL})}{100}\right) \right] \left(\frac{\mathrm{SIL}}{\mathrm{CLA}+\mathrm{SIL}}\right)^{0.3} \\ \left(1-\frac{0.25\;\mathrm{OC}}{\mathrm{OC}+e^{3.72-2.95\;\mathrm{OC}}}\right)\left(1-\frac{0.75\;\mathrm{SN}}{\mathrm{SN}+e^{-5.51+22.9\;\mathrm{SN}}}\right) \end{gathered} \] where \(\SIb{\mathrm{CLA}}{\%}\), \(\SIb{\mathrm{SIL}}{\%}\), \(\SIb{\mathrm{SAN}}{\%}\) are respectively the clay, silt and sand fractions of the topsoil, \(\SIb{OC}{\%}\) is the topsoil organic carbon content and \(\mathrm{SN} = 1-\mathrm{SAN}/100\). These soil parameters can be derived for example from the SoilGrids dataset. The \(K\) factor can also be estimated from the soil mean geometric diameter using the formulation from the RUSLE guide by Renard & al. (1997): \[ \subtext{K}{USLE} = 0.0034 + 0.0405\exp\left(-\dfrac{1}{2}\left(\dfrac{\log_{10}(D_g)+1.659}{0.7101}\right)^2\right) \] where \(D_g\) is the soil geometric mean diameter (mm) estimated from topsoil clay, silt, sand fraction.
| GlobCover Value | Globcover label | \(\subtext{C}{USLE}\) |
|---|---|---|
| 11 | Post-flooding or irrigated croplands (or aquatic) | 0.2 |
| 14 | Rainfed croplands | 0.35 |
| 20 | Mosaic cropland (50-70%) vegetation (grassland/shrubland/forest) (20-50%) | 0.27 |
| 30 | Mosaic vegetation (grassland/shrubland/forest) (50-70%) / cropland (20-50%) | 0.25 |
| 40 | Closed to open (>15%) broadleaved evergreen or semi-deciduous forest (>5m) | 0.0065 |
| 50 | Closed (>40%) broadleaved deciduous forest (>5m) | 0.001 |
| 60 | Open (15-40%) broadleaved deciduous forest/woodland (>5m) | 0.01 |
| 70 | Closed (>40%) needleleaved evergreen forest (>5m) | 0.001 |
| 90 | Open (15-40%) needleleaved deciduous or evergreen forest (>5m) | 0.01 |
| 100 | Closed to open (>15%) mixed broadleaved and needleleaved forest (>5m) | 0.02 |
| 110 | Mosaic forest or shrubland (50-70%) / grassland (20-50%) | 0.015 |
| 120 | Mosaic grassland (50-70%) / forest or shrubland (20-50%) | 0.03 |
| 130 | Closed to open (>15%) (broadleaved or needleleaved, evergreen or deciduous) shrubland (<5m) | 0.035 |
| 140 | Closed to open (>15%) herbaceous vegetation (grassland, savannas or lichens/mosses) | 0.05 |
| 150 | Sparse (<15%) vegetation | 0.35 |
| 160 | Closed to open (>15%) broadleaved forest regularly flooded (semi-permanently or temporarily) - Fresh or brackish water | 0.001 |
| 170 | Closed (>40%) broadleaved forest or shrubland permanently flooded - Saline or brackish water | 0.0005 |
| 180 | Closed to open (>15%) grassland or woody vegetation on regularly flooded or waterlogged soil - Fresh, brackish or saline water | 0.04 |
| 190 | Artificial surfaces and associated areas (Urban areas >50%) | 0.0 |
| 200 | Bare areas | 0.0 |
| 210 | Water bodies | 0.0 |
| 220 | Permanent snow and ice | 0.0 |
| 230 | No data (burnt areas, clouds,…) | 0.0 |
Overland flow erosion
Overland flow (or surface runoff) erosion is induced by the strength of the shear stress of the surface water on the soil. As in rainfall erosion, the effect of the flow shear stress can be reduced by the soil vegetation or by the soil properties. In wflow_sediment, soil detachment by overland flow is modelled as in ANSWERS with (Beasley et al, 1991): \[ D_G = 0.90 \, \subtext{C}{USLE} \, \subtext{K}{USLE} \, A_i \, S \, q \] where \(\SIb{D_F}{kg\;min^{-1}}\) is soil detachment by flow, \(\subtext{C}{USLE}\) and \(\subtext{K}{USLE}\) are the USLE cover and soil erodibility factors, \(\SIb{A_i}{m^2}\) is the cell area, \(S\) is the slope gradient and \(\SIb{q}{m^2 min^{-1}}\) is the overland flow rate per unit width. The USLE \(C\) and \(K\) factors can be estimated with the same methods as for rainfall erosion and here the slope gradient is obtained from the sinus rather than the tangent of the slope angle.
Delivery to the river system
Once soil is detached, it can be transported by overland flow and reach the river system. This process is described in Sediment Flux in overland flow.
References
- D.B Beasley and L.F Huggins. ANSWERS - Users Manual. Technical report, EPA, 1991.
- P. Borrelli, M. Märker, P. Panagos, and B. Schütt. Modeling soil erosion and river sediment yield for an intermountain drainage basin of the Central Apennines, Italy. Catena, 114:45-58,
- 10.1016/j.catena.2013.10.007
- C. Bosco, D. De Rigo, O. Dewitte, J. Poesen, and P. Panagos. Modelling soil erosion at European scale: Towards harmonization and reproducibility. Natural Hazards and Earth System Sciences, 15(2):225-245, 2015. 10.5194/nhess-15-225-2015
- C.J Brandt. Simulation of the size distribution and erosivity of raindrops and throughfall drops. Earth Surface Processes and Landforms, 15(8):687-698, dec 1990.
- K. Chadli. Estimation of soil loss using RUSLE model for Sebou watershed (Morocco). Modeling Earth Systems and Environment, 2(2):51, 2016. 10.1007/s40808-016-0105-y
- G R Foster. Modeling the erosion process. Hydrologic modeling of small watersheds, pages 295-380, 1982.
- A. Gericke. Soil loss estimation and empirical relationships for sediment delivery ratios of European river catchments. International Journal of River Basin Management, 2015. 10.1080/15715124.2014.1003302
- L.D.K. Mansoor, M.D. Matlock, E.C. Cummings, and L.L. Nalley. Quantifying and mapping multiple ecosystem services change in West Africa. Agriculture, Ecosystems and Environment, 165:6-18, 2013. 10.1016/j.agee.2012.12.001
- Q Morgan, J.N Smith, R.E Govers, G Poesen, J.W.A Auerswald, K Chisci, G Torri, D Styczen, and M E Folly. The European soil erosion model (EUROSEM): documentation and user guide. Technical report, 1998.
- S.L Neitsch, J.G Arnold, J.R Kiniry, and J.R Williams. SWAT Theoretical Documentation Version
- Texas Water Resources Institute, pages 1-647, 2011. 10.1016/j.scitotenv.2015.11.063
- P. Panagos, P. Borrelli, K. Meusburger, C. Alewell, E. Lugato, and L. Montanarella. Estimating the soil erosion cover-management factor at the European scale. Land Use Policy, 48:38-50, 2015. 10.1016/j.landusepol.2015.05.021
- K Renard, Gr Foster, Ga Weesies, Dk McCool, and Dc Yoder. Predicting soil erosion by water: a guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE). Washington, 1997.
- D. Torri, M. Sfalanga, and M. Del Sette. Splash detachment: Runoff depth and soil cohesion. Catena, 14(1-3):149-155, 1987. 10.1016/S0341-8162(87)80013-9
- J. de Vente, J. Poesen, G. Govers, and C. Boix-Fayos. The implications of data selection for regional erosion and sediment yield modelling. Earth Surface Processes and Landforms, 34(15):1994-2007, 2009. 10.1002/esp.1884
- G. Verstraeten and J. Poesen. Estimating trap efficiency of small reservoirs and ponds: methods and implications for the assessment of sediment yield. Progress in Physical Geography, 24(2):219-251, 2000. 10.1177/030913330002400204
- O. Vigiak, A. Malago, F. Bouraoui, M. Vanmaercke, and J. Poesen. Adapting SWAT hillslope erosion model to predict sediment concentrations and yields in large Basins. Science of the Total Environment, 538:855-875, 2015. 10.1016/j.scitotenv.2015.08.095
- J.R. Williams, K.G. Renard, and P.T. Dyke. EPIC A new method for assessing erosion’s effect on soil productivity. Journal of Soil and Water Conservation, 38(5):381-383, 1983.
- D. Yang, S. Kanae, T. Oki, T. Koike, and K. Musiake. Global potential soil erosion with reference to land use and climate changes. Hydrological Processes, 17(14):2913-2928, 2003. 10.1002/hyp.1441