Frequently asked questions
How do I easily modify input parameters?
See this section on how to adjust maps, and this section on how to directly pass uniform values. Note that both options work for any parameter.
How do I start wflow with initial conditions from a previous run?
See here
How do I add external inflows and/or abstractions?
river_water__external_inflow_volume_flow_rate: positive for inflows, negative for abstraction. If parameter is time varying, add it to the correct section, see below. Note that these values can only be specified on river cells.
How do I add time-varying parameters?
Either through cyclic (add parameter to cyclic list in the toml), or to the forcing section.
How do I add different output?
See here for csv output, here for scalar netcdf data, and here for gridded netcdf output.
Which river routing option should I choose?
The choice of a specific river routing option can vary depending on the model and use case. However, the numerical properties of the routing schemes provide an indication of their advantages and disadvantages.
The kinematic wave method is driven by the river slope within each cell, assuming that the water surface slope is parallel to the bed slope. This results in sharper discharge peaks with minimal damping, as the waves travel through the system without deformation. This approach is especially suitable for steep (upstream) areas where flow propagation is dominated by topography. The kinematic wave approach does not include any form of backwater effects.
On the other hand, the local inertial method incorporates the slope of the water surface into the momentum equation. This results in ‘damping effects’ on flow propagating through the cells and yields better results in scenarios where the water surface slope differs from the bed slope. This is particularly relevant in flat (downstream) regions where the river slope is limited or during the propagation of larger flood waves where the water surface slope is greater than the river slope itself. The local inertial method does incorporate backwater effects, although not as comprehensively as the full dynamic wave equation.
Generally, the kinematic wave method is computationally faster than the local inertial method for river (and land) routing. For the multi-threading execution of the kinematic wave, solved with a nonlinear scheme using Newton’s method, the order of execution (sub-basins) is important (from upstream to downstream sub-basin). For the momentum equation of the local inertial approach an explicit numerical method is used and can be solved independently for each cell during multi-threading execution. As a consequence, speedups for local inertial routing are larger than for kinematic wave routing using multi-threading (compared to a single thread run) and the difference between local inertial and kinematic wave routing run times gets smaller as the number of threads increase.
Currently, only the local inertial approach supports the inclusion of floodplains in river routing, see also this question.
Which land routing option should I choose?
Similar to river routing, the selection of the type of land routing depends on the model and use case. In practice, the kinematic wave approach is often sufficient for land routing. When the kinematic wave approach is used, water can flow from land cells into river cells, but not the other way around. The local inertial method for land routing is considered in cases where routing occurs over very flat areas or where complicated inundation patterns need to be included in both land and river routing.
The computational differences between the two options are larger than those between river routing options. This is due to the fact that there are typically more land cells than river cells in a model, and that for local inertial land routing two momentum equations (in the x and y direction) need to be solved. Consequently, more equations (with a higher computational cost compared to the kinematic wave method) must be solved compared to the combination of kinematic wave for land routing and local inertial for river routing.
What is the difference between 1D, 2D and no floodplains?
Effects of floodplain flow can be included in several ways. A one-dimensional sub-grid approximation (hence the name 1D floodplains) can be included when kinematic wave land routing is combined with local inertial river routing. The water surface elevations of the river channel and the floodplain are the same and it is assumed that water is exchanged instantaneously between the river channel and the floodplain. When the water depth in the river channel rises above the river bankfull depth, water is exchanged between the river channel and the floodplain resulting in an attenuation of the discharge peaks.

Routing is done separately for the river channel and floodplain, and using this feature does result in larger computational times.
Also for the local inertial approximation of both land and river routing, the water surface elevations of the river channel and the associated land cell (floodplain) are the same and is it assumed that water is exchanged instantaneously between the river channel and associated land cell (floodplain). Between land cells water can flow in two directions (x and y direction) hence the term 2D floodplain method. Additionally, saturation‐excess and infiltration‐excess overland flow are routed in two directions. Note that overland flow can not occur diagonally as opposed to the river routing, which may overestimate flow paths near river cells. Furthermore, as water from the river is exchanged with the full land cell the inundation area can be overestimated, especially for small river channels or land cells with relatively large sub-grid elevational differences. If these limitations are not acceptable, the 1D floodplain method can be used instead.
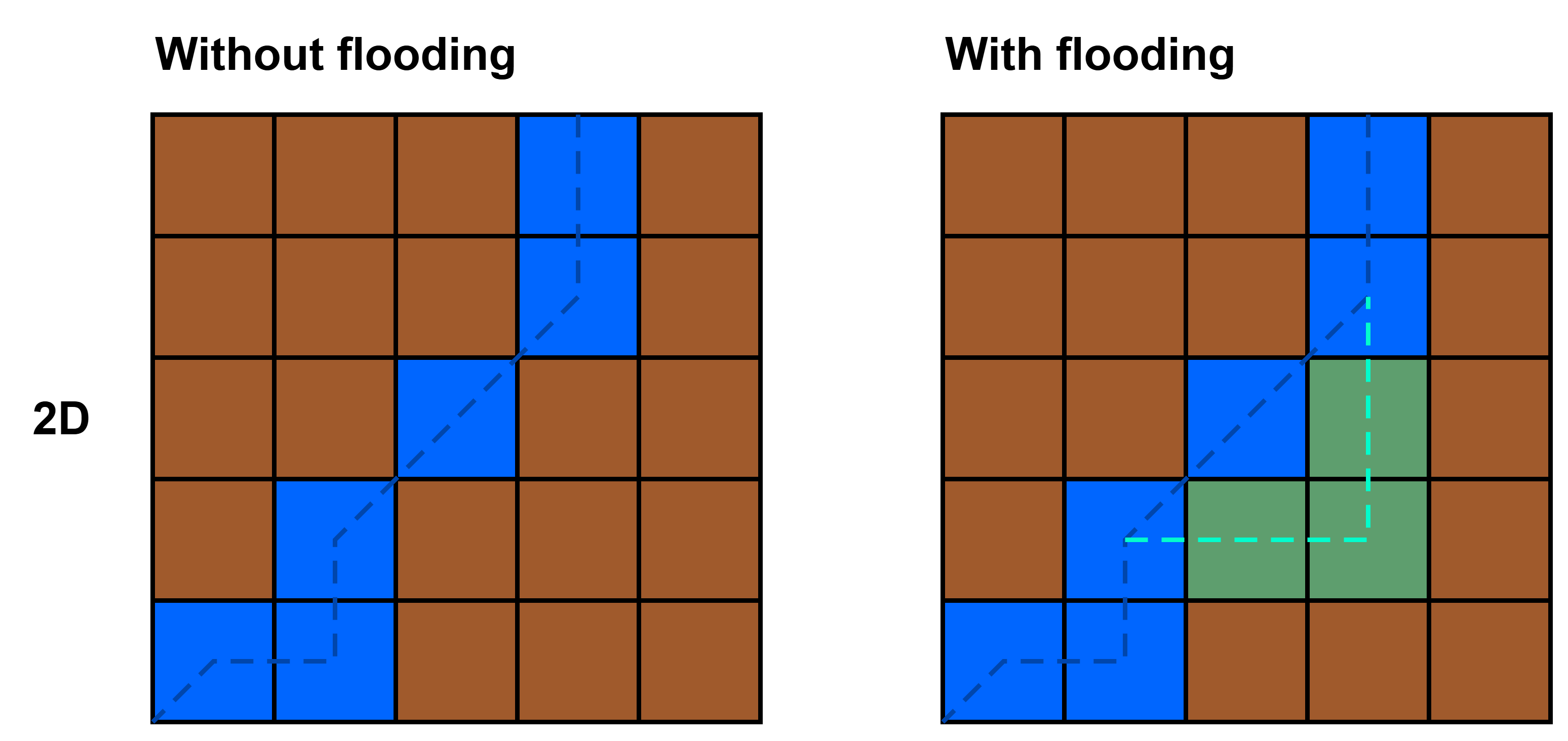
It is also possible to run the model without 1D or 2D floodplains. This means that the model is using kinematic wave for land routing and either kinematic wave or local inertial for river routing. This can lead to unrealistically large water depths when the bankfull capacity is exceeded as there is no exchange of water between the river channel and (1D or 2D) floodplains.